

Rules for Finding Basic Percentages

- To find 1%, divide the number by 100.
- To find 5%, divide the number by 20 or find half of 10%.
- To find 10%, divide the number by 10.
- To find 20%, divide the number by 5 or find 10% and double it.
- To find 25%, divide the number by 4.
- To find 33.̄3%, divide the number by 3.
- To find 50%, divide the number by 2.
- To find 75%, divide the number by 4 and then multiply by 3.


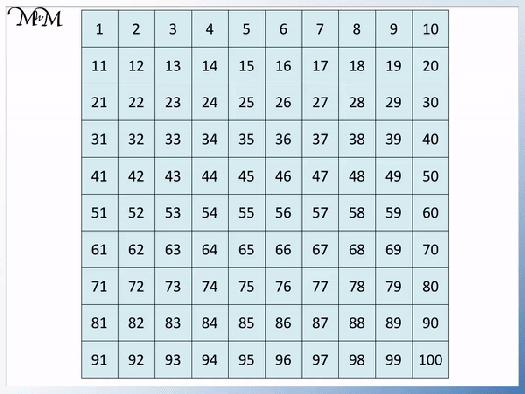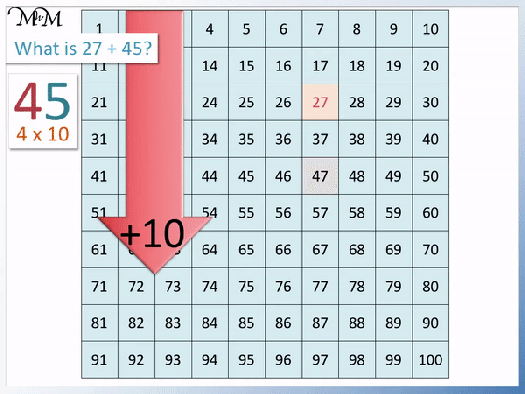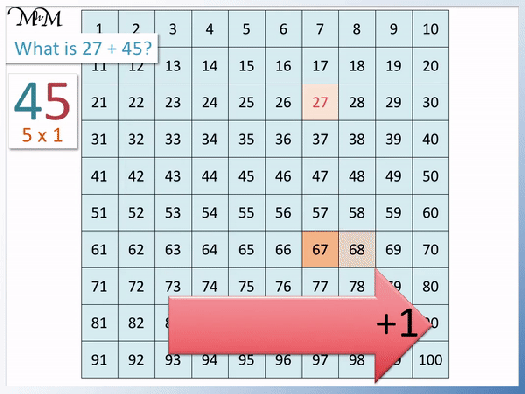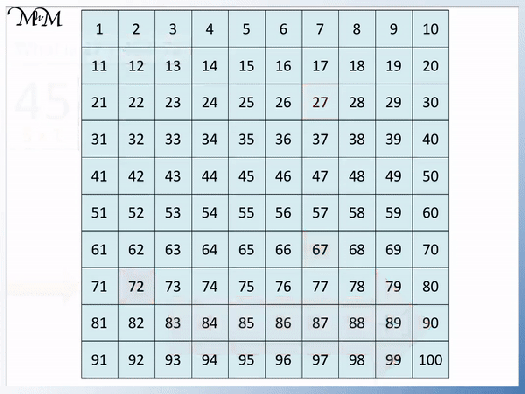
- We want to find 20% of 40.
- To find 20% of a number, divide the number by 5 or find 10% and double it.
- 40 ÷ 5 = 8 and so, 20% of 40 = 8.
- Alternatively, we can find 10% and double it.
- To find 10% of 40, divide it by 10.
- 10% of 40 = 4.
- We double 10% to find that 20% = 8.

Teaching and Introducing Simple Percentages
Finding Simple Percentages: 10%, 25%, 50% and 100%
Finding Simple Percentages: 1%, 5%, 20% and 75%
Finding Multiples of 10%

Calculating Simple Percentages (1%, 5%, 20% and 75%): Interactive Activity
1%, 5%, 20% and 75% of an Amount: Interactive Questions
Calculating Simple Percentages (10%, 25% and 50%) : Interactive Activity
Finding 10%, 25% and 50% of an Amount: Interactive Questions
Calculating Multiples of 10% of an Amount
Multiples of 10 Percent: Interactive Questions
Simple Percentages as Fractions Worksheets and Answers
Simple Fractions of Amounts Worksheets and Answers
Finding Multiples of 10% of a Number Worksheets and Answers
Simple Percentages of Amounts
Rules for Finding Simple Percentages of a Number
The rules for finding simple percentages of a number are shown in the following table:
| Percentage | Rule |
|---|---|
| 1% | ÷ 100 |
| 5% | ÷ 20 |
| 10% | ÷ 10 |
| 20% | ÷ 5 |
| 25% | ÷ 4 |
| 33.̄3% | ÷ 100 |
| 50% | ÷ 2 |
| 75% | ÷ 4 then × 3 |
To find the percentages of a number shown in the table above, simply divide the number using the rules provided.
Simple percentages are percentages of amounts that can be found with a simple division or multiplication. They do not require any addition of any smaller percentages.
For example, 50% is a simple percentage because we simply divide by 2 to find it. 31% is not a simple percentage we would need to calculate 30% and 1% and add them together.
Here is a poster showing how to calculate basic percentages.

To introduce percentages, it is best to start with simple percentages and showing them as a fraction out of 100. For example, 50% means 50 out of 100, which is half. To find 50% of a number, simply half it.
Before looking at larger percentages, it is best to introduce basic percentages with a visual guide to how large they are. To teach how large a percentage is, you can show the percentage as a fraction of 100 squares.

Start by introducing the following percentages first: 10%, 20%, 25%, 50%, 75% and 100%.
How to Calculate 1% of a Number
To calculate 1% of a number, divide the number by 100. To divide by 100, move the decimal point two places left. For example, 1% of 135.6 = 1.356.
1% means 1 out of 100. 1% is the same as the fraction 1/100 .
To teach 1%, we can show 1 square shaded out of 100 squares.

1% means 1/100 and so, finding 1% of a number means to find 1/100 of that number.
To find 1% of a number without a calculator, divide the number by 100. The easiest way to do this is to move the decimal point 2 places to the left.
Here are some examples of finding 1%,
| Question | Answer |
|---|---|
| 1% of 300 | 3 |
| 1% of 150 | 1.5 |
| 1% of 25 | 0.25 |
| 1% of 8 | 0.08 |
| 1% of 3.6 | 0.036 |
| 1% of 0.205 | 0.00205 |
To find 1% of a number with a calculator, divide the number by 100. You can also multiply the number by 0.01.
1% is a basic percentage because it can be found with one simple division. 1% is a very useful percentage to know how to find because you can use it to find any larger, whole number percentage of a number. Simply multiply the percentage required by the value of 1%.
How to Calculate 5% of a Number
To find 5% of a number, divide the number by 20. This can be done by dividing the number by 10 and then halving it. For example, 5% of 40 = 2.
5% means 5 out of 100. 5% is the same as the fraction 5/100 , which can be simplified to 1/20 .
5% is a twentieth of the whole number.
5% means 1/20 and so, finding 5% of a number means to find 1/20 of that number.
To find 5% of a number without a calculator, divide the number by 20. The easiest way to do this is to divide by 10 and then halve the result.
Here are some examples of finding 5%,
To find 5% of a number with a calculator, divide the number by 20. You can also multiply the number by 0.05.
Finding 5% is best to introduce after you have already learnt how to find 10%.
To calculate 10% of a number, divide the number by 10. The easiest way to do this is to move the decimal point one place to the left. For example, 10% of 14.5 = 1.45.
10% means 10 out of 100. 10% is the same as the fraction 10/100 , which simplfies to 1/10 .
To teach 10%, we can show 10 squares shaded out of 100 squares.
10% means 1/10 and so, finding 10% of a number means to find 1/10 of that number.
To find 10% of a number without a calculator, divide the number by 10. The easiest way to do this is to move the decimal point 1 place to the left.
Here are some examples of finding 10%,
To find 10% of a number with a calculator, divide the number by 10. You can also multiply the number by 0.1.
10% is a basic percentage because it can be found with one simple division. 10% is a very useful percentage to know how to find because we can easily multiply 10% to find other multiples of 10%, such as 20%, 30% etc.
To find multiples of 10% of a number, use these rules:
Here is a poster showing how to find all of the multiples of 10% of a number.
For example, to find 30% of 50, divide 50 by 10 to find 10% and then multiply this by 3 to get 30%.
To find 10% of 50, divide it by 10. 10% of 50 = 5.
Now that we have 10%, we simply multiply it by 3 to find 30%. 30% of 50 = 15.
Here is another example of finding a multiple of 10 percent. What is 40% of 70 grams?
To find 40% of a number, divide it by 10 to find 10% and then multiply this by 4.
10% of 70 grams = 7 grams.
To find 40%, we multiply 10% by 4. 40% of 70 grams = 28 grams.
Here we will find 80% of 120.
To calculate 80% of a number, divide the number by 10 to get 10% and then multiply this by 8.
10% of 120 = 12.
80% is 10% multiplied by 8. 80% = 96, therefore 80% of 120 = 96.
To calculate 20% of a number, divide it by 5. Alternatively, divide the number by 10 and then double it. For example, 20% of 30 = 6.
20% means 20 out of 100. 20% is the same as the fraction 20/100 , which can be simplified to 1/5 .
20% is a fifth of the whole number.
20% means 1/5 and so, finding 20% of a number means to find 1/5 of that number.
To find 20% of a number without a calculator, divide the number by 5. Alternatively, divide the number by 10 and then double it.
Here are some examples of finding 20%,
To find 20% of a number with a calculator, divide the number by 5. You can also multiply the number by 0.2.
To calculate 33 1/3 % of a number, divide it by 3.
3 1/3 is the same as 33.̄3%. To find 3 1/3 or 33.̄3%, divide the number by 3.
33.̄3% means 1/3 and so, finding 33.̄3% of a number means to find 1/3 of that number.
To find 33.̄3% of a number without a calculator, divide the number by 3.
To find 33.̄3% of a number with a calculator, divide the number by 3. You can also multiply the number by 0.̄3.
To calculate 50% of a number, divide the number by 2. For example, 50% of 20 = 10.
50% means 50 out of 100. 50% is the same as the fraction 50/100 , which simplfies to 1/2 .
To teach 50%, we can show 50 squares shaded out of 100 squares.
50% means 1/2 and so, finding 50% of a number means to find 1/2 of that number.
To find 50% of a number without a calculator, divide the number by 2. To divide an odd number by 2, subtract one, half it and then add 0.5
Here are some examples of finding 50%,
To find 50% of a number with a calculator, divide the number by 2. You can also multiply the number by 0.5.
To calculate 75% of a number, divide the number by 4 and then multiply this result by 3. For example 75% of 20 = 15.
75% means 75 out of 100. 75% is the same as the fraction 75/100 , which simplfies to 3/4 .
75% is three quarters of an amount.
To teach 75%, we can show 75 squares shaded out of 100 squares. It is helpful to shade the squares in the four corners as shown.
75% means 3/4 and so, finding 75% of a number means to find 3/4 of that number.
To find 75% of a number without a calculator, divide the number by 4 and then multiply by 3.
Here are some examples of finding 75%,
To find 75% of a number with a calculator, divide the number by 4 and then multiply by 3. You can also multiply the number by 0.75.
100% of a number is the whole of the number. 100% means one whole and so, 100% of a number is simply the number itself.
100% means 100 out of 100. 100% is the same as the fraction 100/100 , which simplfies to 1 whole.
We can see in this diagram that 100% shows all 100 squares shaded in.
To find 100% of something simply means to find the whole amount of it. For example, 100% of 25 = 25.

Question
Answer
5% of 200
10
5% of 60
3
5% of 30
1.5
5% of 8
0.4
5% of 1.6
0.08
5% of 0.402
0.0201
How to Calculate 10% of a Number

Question
Answer
10% of 1200
120
10% of 600
60
10% of 50
5
10% of 9
0.9
10% of 5.3
0.53
10% of 0.105
0.0105
Multiples of 10% of a Number
Percentage
Rule
10%
÷ 10
20%
÷ 10 then × 2
30%
÷ 10 then × 3
40%
÷ 10 then × 4
50%
÷ 10 then × 5
60%
÷ 10 then × 6
70%
÷ 10 then × 7
80%
÷ 10 then × 8
90%
÷ 10 then × 9







How to Calculate 20% of a Number

Question
Answer
20% of 400
80
20% of 20
4
20% of 70
14
20% of 5
1
20% of 6.1
1.22
20% of 0.303
0.0606
How to Calculate 33 1/3 % of a Number

How to Calculate 50% of a Number

Question
Answer
50% of 800
400
50% of 300
150
50% of 20
10
50% of 7
3.5
50% of 2.6
1.3
50% of 0.804
0.402
How to Calculate 75% of a Number

Question
Answer
75% of 800
600
75% of 300
225
75% of 60
45
75% of 4
3
75% of 6.8
5.1
75% of 0.334
0.2505
What is 100% of a Number?


Now try our lesson on How to Calculate Percentages of Numbers where we learn how to find any percentage of a number.
































































































































































 We put each group of 3 digits into the groups: HTU, Thousands, Millions and Billions from right to left.
We put each group of 3 digits into the groups: HTU, Thousands, Millions and Billions from right to left.







