

- A multiplication array is a collection of items arranged in rows and columns that represent a number formed from a multiplication of two numbers.
- The number represented is the total number of items in the rectangular array.
- The multiplication represented is the number of items in each row multiplied by the number of items in each column.
- There are 2 items in each column so each array here represents a multiple of 2.
- There is 1 lot of 2 in the first array, which represents the multiplication of 1 × 2 = 2.
- There are 2 lots of 2 in the second array, which represents the multiplication of 2 × 2 = 4.
- There are 3 lots of 2 in the third array, which represents the multiplication of 3 × 2 = 6.
- There are 4 lots of 2 in the fourth array, which represents the multiplication of 4 × 2 = 8.
- Arrays can be used to teach multiplication visually and appreciate the size of the numbers formed in a multiplication.
- Arrays can be used to show how multiplication is the same as repeated addition. In this case, we can see that we add a row of 2 each time.
- Multiplication arrays can be used to provide students with a strategy to work out multiplications that they do not know.
- Arrays can also be used to show how the order in which you multiply two numbers does not matter.


- Here is a multiplication array used to represent the multiplication sentence of 4 x 5 = 20.
- There are 4 counters in each column and there are 5 counters in each row.
- We can see that we have taken the 4 counters in each column and repeated them 5 times.
- We have multiplied 4 by 5.
- There are 20 counters in total, so 4 x 5 = 20.
- The number of counters in each column multiplied by the number of counters in each row must equal the total number of counters.
Multiplication Arrays
What are Multiplication Arrays?
Multiplication arrays are rectangular collections of objects that are used to represent multiplication equations. The number of objects in each row is multiplied by the number of objects in each column to make the total number of objects in the array.
For example, here is the multiplication array showing 4 × 3.

In a multiplication array, the number of items in each row multiplied by the total number of items in each column gives the total number of items.
There are 12 counters in total. The total number of items shown is 12.
There are 4 counters in each row and 3 counters in each column.
The multiplication array shows 4 lots of 3. 3 is mutliplied by 4 to make 12. The multiplication array represents 4 × 3 = 12.
It does not matter in which order we multiply the rows and columns.
Multiplication arrays can be used to show the commutative property of multiplication. The commutative property of multiplication means that it does not matter in which order the numbers are multiplied, the answer is still the same. For example 4 × 3 is the same as 3 × 4.
Here is the same array but grouped to show 3 × 4 instead of 4 × 3.

This time, we can see that we have 3 lots of 4, whereas in the previous animation we have 4 lots of 3.
The result is still the same as the total number of counters did not change. Both 3 × 4 and 4 × 3 = 12.
Why do we Use Multiplication Arrays?
Multiplication arrays are used to introduce the concept of multiplication in a visual way. They help us to visualise the size of numbers produced in multiplication. Multiplication arrays also help us to understand multiplication as repeated addition and that the order in which two numbers are multiplied does not affect the size of the answer.
When teaching multiplication arrays, they can be introduced through the process of repeated addition.
For example, we can start with 2 counters, which represents 1 lot of 2. As we say “1 lot of 2” we can write 1 × 2.
We can then add another lot of two directly next to this to represent 2 lots of 2. As we say “2 lots of 2” we can write 2 × 2.

The same applies for 3 lots of 2, written as 3 × 2 and 4 lots of 2, written as 4 × 2.
When teaching multiplication arrays, it helps to use physical items such as counters. You can also show examples of multiplication arrays in real life.
Some examples of multiplication arrays in real life are:
- The number of eggs in an egg box.
- The number of seats arranged in rows in a classroom.
- The number of cakes placed on a baking tray.
It helps to show examples of arrays in real life to help learn multiplication facts.
Once you have introduced multiplication arrays as repeated addition, you should draw the link between the number of items in each row and each column to form the multiplication sentence.

Show that the number in each row multiplied by the number in each column is the number of counters we have in total.
This means that when you see multiplication arrays in real life, you can practice working out how many items there are in total by multiplying the number in each row by the number in each column.
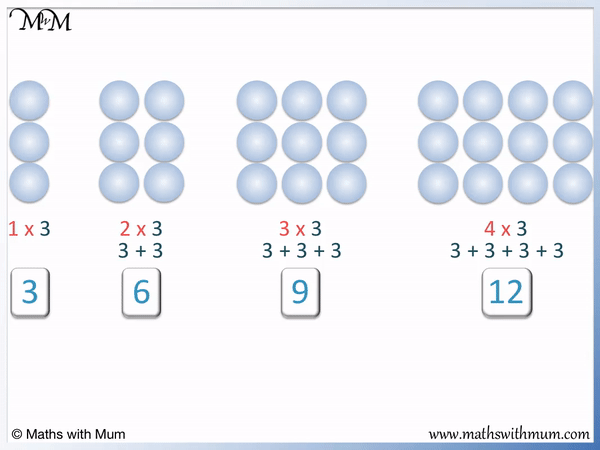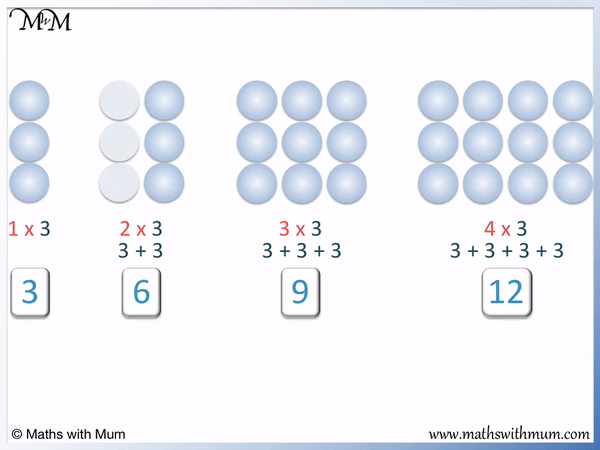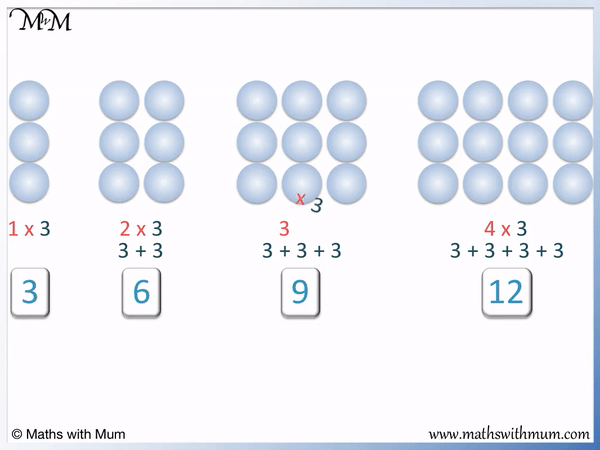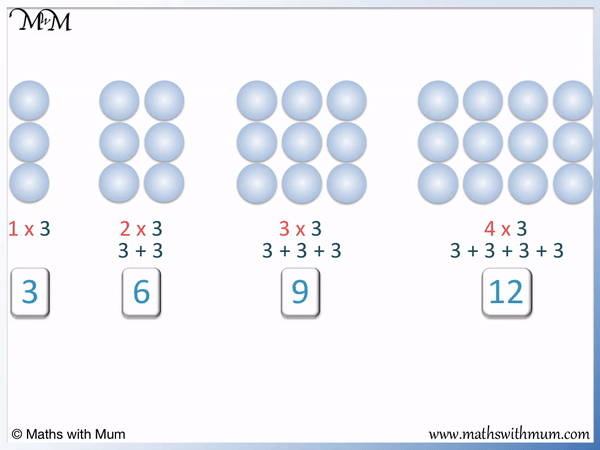
Here is a similar example with the start of the 3 times table.

1 lot of 3 is 3 and so, we write 1 × 3 = 3.
2 lots of 3 is 6 and so, we write 2 × 3 = 6.
3 lots of 3 is 9 and so, we write 3 × 3 = 9.
4 lots of 3 is 12 and so, we write 4 × 3 = 12.
Multiplication arrays can also be used to teach the commutative property of multiplication. The commutative property of multiplication simply means that the order in which two numbers are multiplied does not affect the size of the answer. For example,

Here we have 6 multiplied by 10. We can see that we have 10 lots of 6 counters. There are 60 counters in total.

Here we have 6 lots of 10.
The result is still the same as the total number of counters did not change.

Now try our lesson on Multiplication as Equal Groups where we learn how multiplication can be used to represent equal groups of a number.





