What is the Commutative Property?
The commutative property simply means that switching the order of the numbers in a calculation does not affect the answer.
Addition and multiplication are both commutative. Subtraction and division are not commutative.
We can remember that the word ‘commute’ means to move. If moving the numbers in a calculation by switching their places does not affect the answer, then the calculation is commutative.
Addition is commutative. For example, 3 + 5 = 8 and 5 + 3 = 8.

We can see that 3 + 5 = 5 + 3.
The commutative law of addition states that a + b = b + a.
‘a’ and ‘b’ are just different numbers and the commutative law means that if we switch the order of the numbers in an addition, the answer remains the same.
Multiplication is commutative. For example, 3 × 5 = 15 and 5 × 3 = 15.

We can see that 3 × 5 = 5 × 3.
The commutative law of multiplication states that a × b = b × a.
‘a’ and ‘b’ are just different numbers and the commutative law means that if we switch the order of the numbers in a multiplication, the answer remains the same.
Is Addition Commutative?
Addition is always commutative. This means that it does not matter in which order two or more numbers are added together, the answer will be the same.
Switching the order of any two numbers in an addition does not affect the answer.
For example 4 + 6 = 10 and 6 + 4 = 10. Both additions are the same except for the two numbers in the addition, 4 and 6, have switched positions. The answer to both sums is both 10.

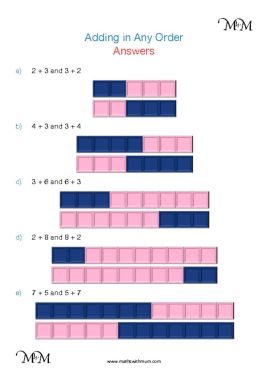
We can teach the commutative property of addition by using multilink cubes or counters.
To show the addition of 4 + 6, we take 4 cubes of one colour and 6 cubes of another. We connect them together to show the addition.
We can see that 4 + 6 = 6 + 4 because both rows of cubes are both the same length. Both rows of cubes are 10 cubes long. 4 + 6 = 10 and 6 + 4 = 10.
The order of addition does not matter.
Here is another example of teaching the commutative property of addition.
We have 3 + 5 and 5 + 3.

We can see that both 3 + 5 = 8 and 5 + 3 = 8.
When teaching commutativity with cubes, we can see that both rows of cubes are the same length.
We can see that as long as the numbers being added are the same, it does not matter which order they are in, the answer is always the same.
Both sums have 3 and 5 next to the addition sign and so, both answers are 8.
When teaching commutativity in addition, multilink cubes are the best because they connect together without gaps.
We can also teach this property using counters as seen in the example of 3 + 2 below.

We can see that there are the same number of counters in each pile.
We can use two piles of counters to show each sum. We can use this to show that 2 + 3 = 3 + 2.
There are 5 counters in both piles.
Is Subtraction Commutative?
Subtraction is not commutative. This means that the order of the numbers in the subtraction does matter.
For example, 10 – 2 = 8 but 2 – 10 = -8. Switching the order of the numbers in the subtraction changed the answer.
We can look at the subtraction 10 – 2 by using counters.
10 – 2 means to start with 10 and take 2 away.
We can see that after removing 2 counters, 8 counters remain.

We can switch the order of the 10 and the 2 in the subtraction.
We will try and work out 2 – 10.
We cannot subtract 10 counters because we do not have enough. We only have 2.
We will not look at negative numbers in this lesson and so, we cannot take away a larger number from a smaller number.
We can see that the order of the subtraction matters. We need to subtract the smaller number from the larger number.
When teaching the order of numbers in a subtraction, we can say that the largest number must come first in a subtraction.

We can subtract 2 from 10 because 10 is larger than 2.
We cannot subtract 10 from 2 because if we only have 2 counters, we will run out before we subtract all 10.
After taking away 2 counters, we would still need to subtract another 8 more. We can say that we would owe 8 counters.
We can write this as 2 – 10 = -8, which means 2 counters subtract 10 counters means that we owe another 8 counters.
We will not introduce negative numbers in this lesson. Instead we will just say that we cannot subtract a larger number from a smaller one without being in debt.
There is no commutative law of subtraction because a – b ≠ b – a..
The order of subtraction matters.
Here is another example in which the order of subtraction matters.
Here is 6 – 5.
We are subtracting a smaller number away from a larger number.
We can teach the order of subtraction with counters by starting with the 6 counters and subtracting 5 to see how many are left over.
After subtracting 5 counters, 1 counter remains.
6 – 5 = 1

If we switch the order of the numbers in a subtraction, the answer is not the same.
5 – 6 does not equal 1.
We can start with 5 counters and try to take away 6 counters but we will run out of counters before we subtract all 6.
Again, without going into debt or negative numbers, in a subtraction the largest number comes first.

6 is bigger than 5 and so, 6 belongs at the front of the subtraction.
It is possible to have 5 – 6 but the answer is -1.
When first teaching subtraction, it can help to show children that the largest number comes first. When negative numbers are introduced at a later stage, this rule is no longer true.









































































 When we divide one half by 3, we split it into 3 equal parts.
When we divide one half by 3, we split it into 3 equal parts.