How to Divide Fractions by Whole Numbers
To divide fractions by whole numbers use the following steps:
- Divide the top of the fraction by the whole number if it divides exactly.
- If not, multiply the bottom of the fraction by the whole number.
If you used step 2, you may need to simplify your answer by dividing the top and bottom of the fraction by the same number.
For example, calculate 4 / 5 ÷ 3.
We first look to see if we can divide the numerator on top by 3.
We have a 4 on the top of the fraction and 4 cannot be divided exactly by 3 to leave a whole number.
This means that we use step 2 instead to divide the fraction.

We multiply the denominator on the bottom by the whole number we are dividing by. 5 is the denominator of the fraction.
5 × 3 = 15 and so, 15 is the denominator on the bottom of the answer.
4 / 5 ÷ 3 = 4 / 15 .
We have multiplied the denominator by 3 to divide the whole fraction by 3.
Calculate 6 / 7 ÷ 2.
We can follow the method shown in the previous example, where we can multiply the denominator by 2.
6 / 7 ÷ 2 = 6 / (7 × 2) .
6 / 7 ÷ 2 = 6 / 14 .
This can then be simplified because both 6 and 14 can be divided by 2.
6 / 14 = 3 / 7 .
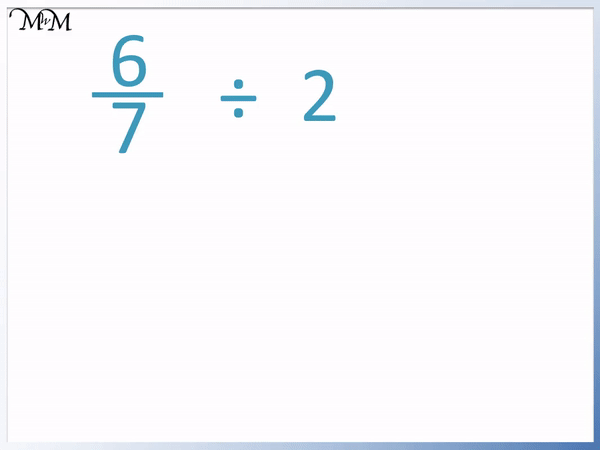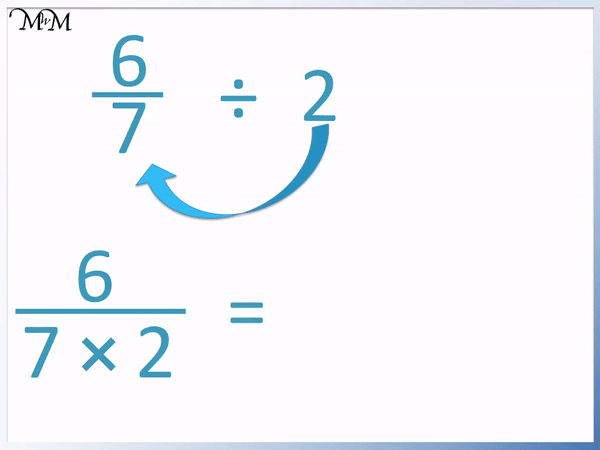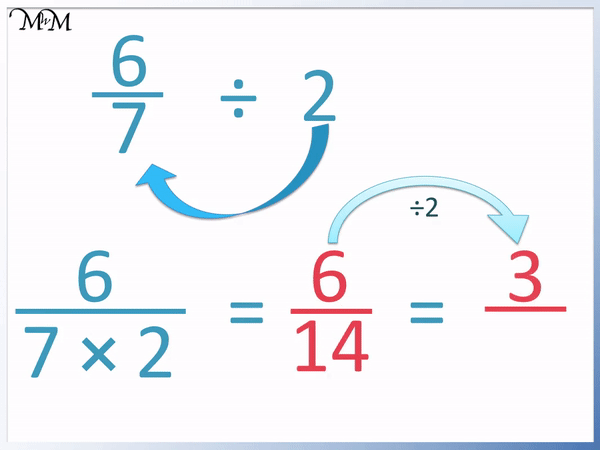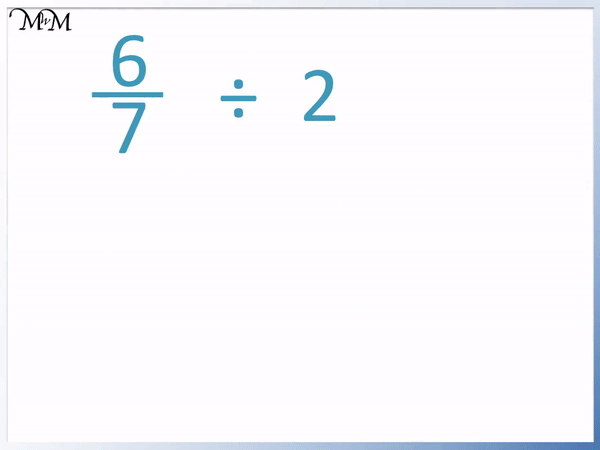
However, it is much easier to use step 1 in our steps for dividing fractions by whole numbers.
We can see that the numerator on top can be divided straight away.
6 ÷ 2 = 3 and so, the numerator can be divided exactly.
We can simply divide the numerator in 6 / 7 by 3 to get our answer of 3 / 7 .
It is easier to do this method as there is no simplification required afterwards.
To divide a fraction by a whole number, we can either multiply the denominator by the whole number or we can divide the numerator by the whole number.
Notice that we only need to do one method or the other.
Here is another example of using this method to divide a fraction by a whole number.
We have 9 / 10 ÷ 3.
We can immediately see that 9 ÷ 3 = 3 and it divides exactly. We use method 1.

We divide the numerator and leave the denominator the same.
9 / 10 ÷ 3 = 3 / 10 .
Notice that we only divide the 9 by 3. We do not multiply the 10 on the bottom by three because we have already done our division by dividing the 9 by 3.
Model for Dividing Fractions by Whole Numbers
When we divide we are sharing an amount into equal parts. Dividing a fraction by a whole number also means to split it into equal parts.
When we divide a fraction by a whole number it gets smaller.
Here is an example of dividing the fraction 1 / 2 by 3.
1 / 2 means that we have 1 out of 2 equal parts.
 When we divide one half by 3, we split it into 3 equal parts.
When we divide one half by 3, we split it into 3 equal parts.

The answer is smaller than one half.
It is 1 out of 6 equal parts.

We say that 1 / 2 ÷ 3 = 1 / 6 .
We can see in the visual model that final shaded area is a smaller fraction than we started with but the number at the bottom of the fraction increased from 2 to 6.
We multiplied the denominator on the bottom of the fraction by 3 to divide the fraction by 3.

Without drawing a visual model, the method is simply to multiply the bottom of the fraction by 3.
Here is another example of dividing a fraction by a whole number.
We have 3 / 4 ÷ 2 = shown with a visual model.
3 / 4 means that we have 3 out of 4 equal parts. This is shown below.

When we divide 3 / 4 by 2, we will only have half of the original shaded fraction.
We can split each quarter in two so that there are 8 pieces in total. 3 quarters is the same as 6 out of 8 parts.
If we divide by 2, we will only have 3 out of 8 parts.
We can see that half of 3 / 4 is 3 / 8 .
The circle was divided into twice as many parts. Instead of 3 out of 4 we now only have 3 out of 8 parts.
We can see this division without a visual model below.

We can see that it is easier to simply multiply the bottom of the fraction by 2. Multiplying the bottom of the fraction by 2 has the same effect as dividing the fraction by 2.
When teaching dividing fractions by whole numbers, it is important to remember that increasing the number on the top of the fraction makes the fraction bigger but increasing the number on the bottom of the fraction makes it smaller.
Some children can be confused with the division resulting in multiplying the denominator on the bottom but it is important to remember that the number on the bottom of the fraction is how many parts we have shared our amount into.
The bigger the denominator on the bottom, the smaller the fraction.





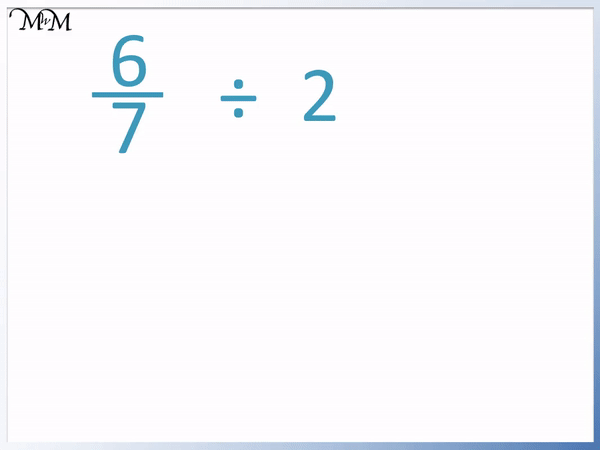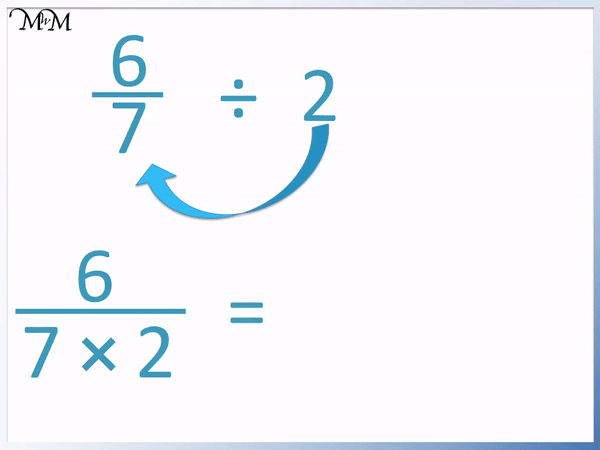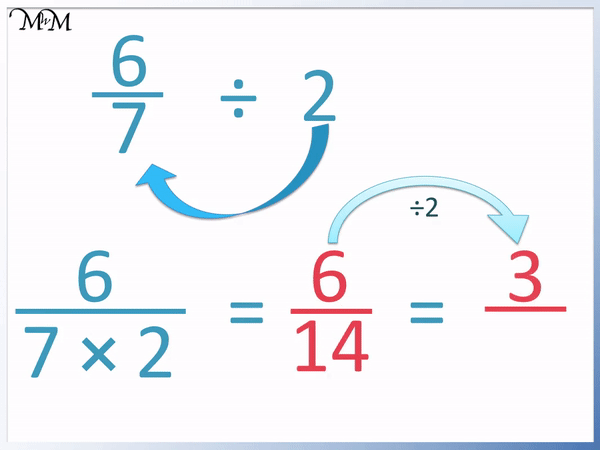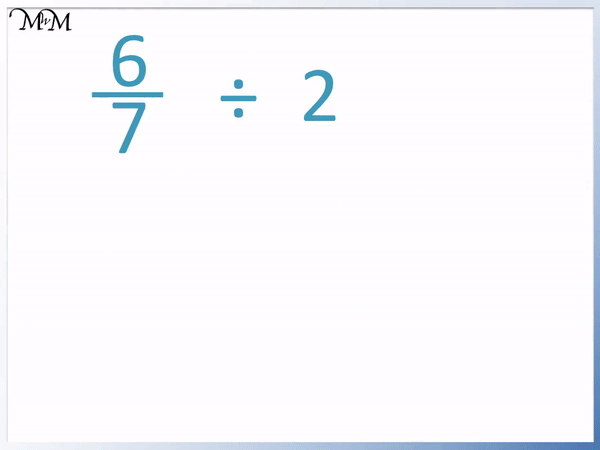






 When we divide one half by 3, we split it into 3 equal parts.
When we divide one half by 3, we split it into 3 equal parts.




