Examples of Counting Amounts of Money

Adding US Money by Regrouping Cents to Dollars

We want to find the total amount of money shown.

We have a dollar bill, three dimes, a nickel and two penny coins.

The dollar bill is worth 100 cents.

Each dime is worth 10 cents, so three dimes are 30 cents.

The nickel is worth 5 cents.

The two penny coins are worth 2 cents in total.

We add the total using column addition to get 137 cents.

We can write this in dollars as $1.37 by dividing 137 by 100

We add the cents up and convert the value to dollars by dividing by 100.

We write our answer with a dollar sign, ‘$’ and no longer write the cent sign, ‘¢’.

Adding Dollars and Cents Example

We will count the amount of money shown.

We have one dollar bill, two dimes and four nickels.

The dollar bill is worth 100 cents.

The two dimes are worth 20 cents because 2 x 10 = 20.

We can add the dollar and the two dimes to make 120 cents.

The four nickles are worth 20 cents because 4 x 5 = 20.

We add this 20 cents to our existing 120 cents to make 140 cents in total.

We divide 140 cents by 100 to convert our value in cents to a value in dollars.

We have $1.40.

Supporting Lessons

Adding American Money

To add money, write the values of each coin and then add the numbers using vertical addition. It is useful to collect the coins into groups that form a multiple of ten cents or a dollar.

In this lesson, we learn how to add dollar bills and count cent coins to make a total.

In the example below, we have some American money. We will add the values of the cent coins to the value of the dollar bill to see how much money there is in total.

We can do this by first adding up our total entirely in cents.

writing the dollar bill as 100 cents to make a total of 137 cents

There is a $1 bill, which is worth 100¢.

The dollar is larger in value than the American cent coins and so we write this 100 cents first.

We then have three one dime coins (each worth 10¢), one nickel (worth 5¢) and two penny coins (each worth 1¢).

To add up our total we use vertical column addition.

We can add the ‘ones’ column:

0 + 0 + 5 + 1 + 1 = 7.

We now add the ‘tens’ column:

0 + 3 = 3.

In the hundreds column, we only have 1.

Therefore our total value of money is 137¢.

adding an amount of money to make a dollar 37 cents

If the total amount of money is more than 100 cents in value, we usually write this amount of money in terms of how many dollars we have. We will convert our total cents into dollars.

There are one hundred cents in a US dollar.

To convert from cents to dollars, we divide by 100.

137 ÷ 100 = 1.37

We write our total as $1.37. We separate the dollars and the cents with a decimal point.

So, we say we have one dollar and thirty-seven cents. You will notice that we only write the dollar sign, ‘$’ in front of our total and if we choose to write our amount in dollars, we do not write the cent sign, ‘¢’ anymore.

We write how many dollars we have made in front of the decimal and then the two digits that come after the decimal point represent how many more cents that we have.

Below, we have another example of counting US money:

2 dollars and 5 cents found by counting dollar bills and US cent coins

There are two $1 notes, which are each worth 100¢. There are also five 1¢ coins, which are worth 5¢ in total.

We write the largest values of money first.

Using column addition, we will add up the total of our money.

In the ‘units’ column of our cents we have:

0 + 0 + 5 = 5

We have no ‘tens’.

Counting the ‘hundreds’ column, we have:

1 + 1 = 2

In total, the amount of money is 205 cents.

Remember that we usually write our amount of money in terms of dollars if we have more than 100 cents in total.

finding the total of an amount of money to be 2 dollars and 5 cents

There are one hundred cents in a US dollar, so to convert our cents to dollars, we divide the amount by 100.

205 ÷ 100 = 2.05

So we can write our total as $2.05.

We can say that we have two dollars and five cents.

When converting our cents to dollars and then writing our answer in dollars, we always write two digits after the decimal point. However, the five cents is only one digit.

Therefore, we must keep the zero in front of the five to ensure that there are two digits after the decimal point.

And so, we write this as $2.05. We separate the dollars and the cents with a decimal point.

Adding Dollars and Cents

To add amounts of money that contain both dollars and cents, it is helpful to count the dollars separately to the cents and add them at the end. It is also useful to count the cents in groups that make multiples of ten cents or a dollar. Add the larger value coins first.

To help count the cent coins, it is useful to know the groups of coins which make a dollar.

Ways to make 1 dollar summary.gif

The dollar bill is worth 100 cents.

The following amounts of money can be replaced with a dollar:

100 penny coins
10 dimes
20 nickels
4 quarters

Any combination of coins that make 100 cents can be replaced with one dollar.

Here is an example of adding a sum of money involving dollars and cents.

Adding US Money Example

To add this sum of money, separate it into dollars and cents.

There are 2 dollar bills and the rest are coins.

We look for groups of coins that add to make a dollar. We have ten dimes.

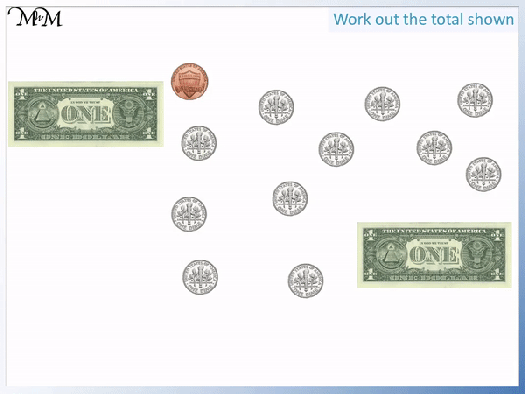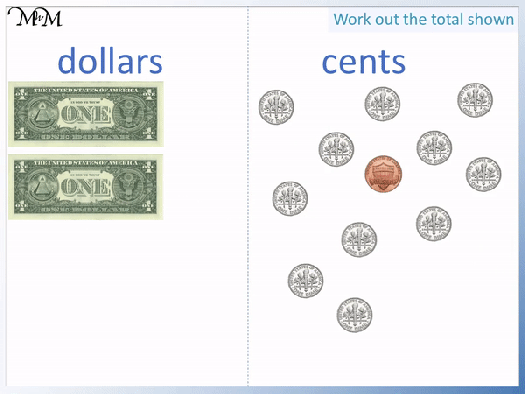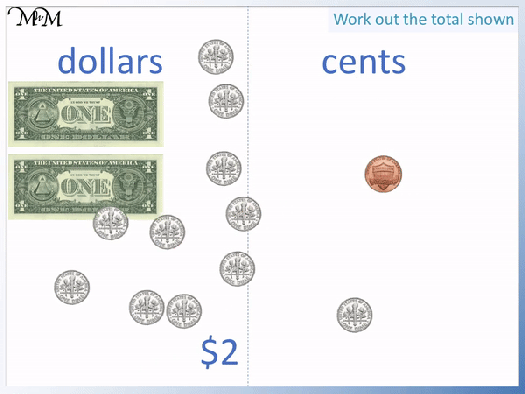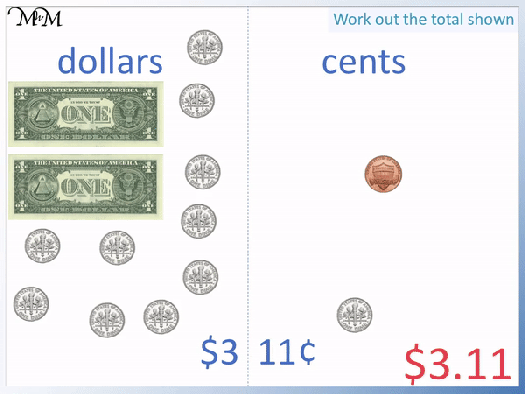
We can move these across to the dollars pile to make $3 in total.

We have a dime and a penny left over. This is worth 11 cents.

There is $3.11 in total.

When teaching children to add money, it is helpful to count the dollars and cents separately. This provides them with a strategy to use to break down the process.

In the example below, there is some American money. We are asked to work out how much money there is in total.

We will start by separating the money into dollars and cents.

american money separated into dollars and cents

We can now add the money by first counting the dollars and then counting the cents.

finding a total of $2.30 two dollars thirty cents, by counting the dollar bills and cent coins separately

Looking at the dollars on the left, we can see that there are two one dollar bills. So, this is worth a total of $2.

Looking at the cent coins that we have, we can see that there are three dimes. Each dime is worth 10¢. So, this is worth a total of 30¢.

Altogether, we have two dollars and thirty cents.

We write this as $2.30, separating the dollars and cents with a decimal point.

We can think of the digit before the decimal representing how many dollars we have and then the two digits after the decimal representing how many cents we have.

In some cases, there will be a group of cent coins that can make another dollar.

an example of some us money that we can count

We will begin by separating the US money into dollar bills and cent coins.

Now we have separated the paper notes from the coins, we will count the dollar bills.

There is a one dollar bill, so we have $1 in total from the paper bills.

Next, we will count the cent coins.

Remember that we are looking out for any of the combinations of coins that can add up to make a dollar.

We can make a dollar from any combination of coins that add up to 100 cents.

A tip for teaching this topic of counting money is to look for the largest value coins first as they will help us to reach 100 cents faster.

$2.20 where one dollar is made from regrouping four quarter dollar coins.

The cent coin with the largest value is the quarter.

Looking at this group of cent coins, we can see that we have four of these quarter dollar coins.

These four quarters make a total of one dollar.

This is because they are each worth 25¢ and

4 x 25¢ = 100¢.

We can move these four coins over to the dollars. We now have $2; one dollar from the paper bill and one dollar made from the four quarter dollar coins.

We can say that we have collected the four quarters into a group of one dollar. When teaching this in schools, this process may be referred to as ‘regrouping’ or ‘carrying’, since we have regrouped 100 cents into 1 dollar.

Finally, we’ll look at the cent coins that remain.

Looking at the cents, we can see that we have two dimes remaining. Each dime is worth 10¢. So, two dimes are worth a total of 20¢.

Altogether, we have two dollars and twenty cents. We write this total as $2.20.

Remember that the ‘2’ in front of the decimal point tells us the total amount of dollars that we have made and the ’20’ after the decimal point tells us that we have twenty cents on top of this.

Below, is our final example of adding money with regrouping.

a collection of american coins where coins will add up to make more than one dollar

Again, we begin by separating the money into paper dollar bills and cent coins.

dollar and cents collected into separate groups

Looking at the dollars, we can see that we have a one dollar note. This is a total value of $1.

Next, we’ll look to see if we can make another dollar out of any of the coins that we have. This means that we need to make a total of 100 cents by adding up the coins.

Remember that when teaching this topic, we encourage you to look for the coins with the largest value first as they bring us closer to 100 cents in the fastest way.

US money with a dollar bill plus another dollar made by collecting cent coins that add to make a total of 100 cents.

Our largest value cent coin is the quarter. There are two quarter dollars, each worth 25¢.

25¢ + 25¢ = 50¢

So far we have 50¢.

Our next largest value coin is the dime, so we now look to move the dimes over until we get to 100 cents or until we run out of dimes.

We have four dimes in total. Each dime is worth 10¢, so four dimes are worth a total of 40¢.

50¢ + 40¢ = 90¢

So far we have 90¢.

We need 10¢ more.

The next largest value coins are nickels, which are each worth 5¢.

So, two nickels are worth a total of 10¢.

90¢ + 10¢ = 100¢

100¢ = $1

Having moved these two nickels over, we have a total of 100¢. We only moved two nickels over, we left another two nickels behind as we made 100 cents without them.

There are 100¢ in a dollar. So, in total, we now have $2. One dollar from the paper dollar bill and one dollar from the collection of different coins that made 100 cents.

Now, we will count the cents that are remaining on the right.

$2.14 with a collection of cent coins regrouped to make 100 cents and therefore a value of one of our dollars

There are two nickels which are each worth 5¢.

5¢ + 5¢ = 10¢

Two nickels are worth 10¢ in total.

We also have four pennies. These are each worth 1¢.

4 x 1¢ = 4¢

Four pennies are worth 4¢ in total.

Two nickels plus four one cent coins make a total of 14¢.

10¢ + 4¢ = 14¢

Altogether, we have two dollars and fourteen cents.

We write this as $2.14.

Now try our lesson on Adding US Money by Regrouping Cents to Dollars where we learn how to regroup cents to make a dollar and use this to work out larger totals of money.

How to Make a Dollar with Coins

usmoneysummary

Here are some common combinations of ways to make a US dollar by making a total of 100 cents.

A dollar is worth 100 cents and each dollar bill is the same value as 100 penny coins.

Each dime is worth 10 cents so ten dimes make one dollar because 10 x 10 = 100 cents.

Each nickel is worth 5 cents so twenty nickels make one dollar because 20 x 5 = 100 cents.

Each quarter is worth 25 cents. 4 x 25 = 100 cents and so four quarters make one dollar.

usmoneyexample

We are asked to count the American money shown.

We have one US dollar bill.

We have four quarters which is one of the combinations of coins that make an American dollar.

We have a dollar bill plus another dollar from the four quarters.

We have two dollars in total, which we can write as $2.

Supporting Lessons

Counting US Money Dollars and Cents: Interactive Question Generator

Counting Money Dollars and Cents: Interactive Question Generator

Adding US Dollars and Cents Worksheets and Answers

Adding American Money: Dollars and Cents

How to Make an American Dollar using Cents, Nickels, Dimes and Quarters

A dollar can be made from any combination of coins that add up to make 100 cents. Here are some common ways to make a dollar with change:

100 pennies

4 quarters

10 dimes

20 nickels

3 quarters, 2 dimes and a nickel

2 quarters and 5 dimes

There are many other ways to make a dollar and we will look at some of the common ways below.

Below is an American one dollar bill, which we commonly refer to as a dollar or US dollar.

Each dollar is worth 100 cents and each dollar bill holds the same value as one hundred cents. A dollar is therefore the same worth as one hundred 1¢ coins combined.

Instead of carrying one hundred 1¢ coins, we can use the one dollar note.

an american one dollar bill banknote

The symbol for a dollar is ‘$’.

Since one dollar is worth 100 cents we can write:

$1 = 100¢.

the dollar symbol

There are many different ways that we can make $1. We can make a dollar by using any combination of US coins that add up to 100¢.

One way to make a dollar is to use 100 cent coins.

one dollar is worth 100 cents

Another way that we can make a dollar is with ten 10¢ coins (ten dimes).

ten dimes are worth one us dollar

This is because each dime is worth ten cents:

10¢ + 10¢ + 10¢ + 10¢ + 10¢ + 10¢ + 10¢ + 10¢ + 10¢ + 10¢ = 100¢

10 x 10¢ = 100¢

one dollar is worth 10 dimes

Another way to make a dollar is to use twenty nickel coins, which are each worth 5¢.

one dollar is worth 20 nickels

This is because 20 x 5 = 100.

twenty nickels are worth one us dollar

20 x 5¢ = 100¢

100¢ = $1

Another way to make a dollar is with four quarter dollar coins. Each quarter is worth 25¢.

The name ‘quarter’ helps us to remember that four quarters make a whole dollar.

four quarters are worth a dollar

25¢ + 25¢ + 25¢ + 25¢ = $1

4 x 25¢ = 100¢

100¢ = $1

one dollar is worth four quarters

Examples of Counting Amounts of Money

In the example below, we are asked to work out the total amount of money. We count any coins that we have into groups that make one dollar.

counting the four quarter dollar coins to make one dollar plus the dollar bill makes two dollars in total

We have a $1 bill and four quarter dollar coins. The four quarter dollar coins add to make a dollar because 4 x 25¢ = 100¢.

For every 100 cents that we can make, we have made one dollar.

We have a one dollar note plus the dollar made from the four quarters.

Altogether, we have $2.

counting an amount of money worth 2 dollars

In the example below, we have two $1 bills and twenty nickels (each worth 5¢).

two dollar bills plus twenty nickels makes 3 dollars because twenty nickels make one dollar

Twenty nickels make one dollar. Each nickel is worth 5 cents and therefore we have $1.

Altogether, we have three American dollars, $3.

an example of counting an amount of money in dollars

Now try our lesson on Adding American Money: Dollars and Cents where we learn how to add dollar bills and cent coins.

Adding US Money Dollars and Cents: Question Generator

Adding US Money Dollars and Cents: Question Generator Return to Video Lesson on: How to Make a Dollar with Coins

What is the total sum of the coins below? Enter your answer in dollars with a decimal point.

Click on each value as you count it.

Counting US Coins: Dimes, Nickels, Pennies & Quarters

US Cent coins value and worth summary poster

This poster shows the values of the four common coins used in America.

The value of each coin is based on how many cents it is worth.

The Penny is worth 1 cent.

The Nickel is worth 5 cents.

The Dime is worth 10 cents.

The Quarter is worth 25 cents.

There are four main American coins: the penny, the nickel, the dime and the quarter.

Example of adding american coins

We have the following American coins: one quarter, one nickel, one dime and three one penny coins.

One quarter is worth 25 cents.

One nickel is worth 5 cents.

We can add these two coins to make a multiple of ten. 25 + 5 = 30 cents.

One dime is worth 10 cents. We add this coin to our total so far.

30 + 10 = 40 cents.

We have three one penny coins left to add to our total.

The total of the coins is 40 + 3 = 43 cents.

Supporting Lessons

Adding American Money: Interactive Activity

Adding American Coins Worksheets and Answers

How to Make a Dollar with Coins

Values of Pennies, Nickels, Dimes and Quarters

Value of a Penny Coin

The penny coin is also known as the one-cent coin. The penny coin is worth one cent and it is the American coin of lowest value. One hundred cent coins make a dollar.

Here is a picture of the one-cent penny coin.

an american one cent coin also known as a penny coin

The cent symbol is ‘¢’ and so we can write one cent as 1¢.

One hundred cents make one dollar.

In dollars, one cent is written $0.01.

Value of a Nickel Coin

The nickel is an American coin that is worth 5 cents. A nickel is worth 5¢ or $0.05.

Here is a picture of a nickel coin.

an american five cent nickel coin

The President Thomas Jefferson is the man on the nickel.

One nickel coin is worth the same as five 1 cent coins.

a nickel is worth the same as 5 cent coins

A nickel is worth 5¢, which can also be written in dollars as $0.05.

Because one hundred cents make a dollar and 20 × 5 = 100, there are 20 nickels in a dollar.

Intro to US Money 1

Value of a Dime Coin

A dime is worth 10 cents. A dime is worth 10¢, which can be written in dollars as $0.10. Ten dimes are worth one dollar.

Here is a picture of a dime.

an american dime coin

The dime coin is worth the same as ten one cent coins.

american dime coin is worth 10 cents

a dime is worth the same as ten one cent coins

A dime is worth 10 cents and a nickel is worth 5 cents. Therefore two nickels are worth the same as one dime.

two nickels are worth the same as a dime because 5 cents + 5 cents = 10 cents

Both the nickel and dime coins are silver in colour but the main difference between them is the size. Although the dime is worth more, it is smaller than the nickel coin.

a dime is worth the same as two nickels

Value of a Quarter Dollar Coin

The quarter is an American coin worth 25 cents. The quarter is worth 25¢, which can be written in dollars as $0.25. Four quarters are worth one dollar.

Here is a picture of the quarter dollar coin.

a quarter dollar coin

A quarter dollar is worth the same as 25 one cent coins.

value of a quarter shown in cents

a quarter is worth 25 cents

A quarter is worth 25¢ and can be made from any combination of coins that add up to make 25 cents.

For example, a quarter dollar can be made from two dimes plus one nickel.

Each dime is worth 10¢ and the nickel is worth 5¢.

10 + 10 + 5 = 25 and so two dimes plus a nickel add up to make 25¢.

a quarter dollar coin is worth the same value as two dimes plus one nickel

Starting with 25 one cent coins, we can see that ten one cent coins can be replaced with a dime and five one cent coins can be replaced with a nickel.

two dimes and a nickel are worth one quarter.

Counting American Coins

We can use the values of the individual US coins to help us work out the totals of different combinations of coins.

We just need to remember the following values:

A one cent coin is worth 1¢
A nickel is worth 5¢
A dime is worth 10¢
A quarter is worth 25¢

In this example we have a quarter, a dime, a nickel and three one cent coins.

It is easiest to start with the largest value coins first.

example of adding american coins

We have a quarter which is worth 25¢.

We try to add coins to make multiples of 10 if we can.

We can add the nickel to the quarter. 5 + 25 = 30 and so 5¢ + 25¢ = 30¢.

We can easily add the dime to this total by adding 10¢.

30 + 10 = 40 and so 30¢ + 10¢ = 40¢.

Finally, we add the cent coins, which are each worth 1¢.

We have 3 one cent coins, worth 3¢ in total.

40 + 3 = 43 and so we have 43¢ in total.

Now try our lesson How to Make a Dollar with Coins where we learn the combinations of different American coins that can make a dollar.

make a dollar with coins

Counting British Coins: Adding Pounds and Pence

how to make a pound in coins

£1 is worth 100 pence and here are some common ways to make one pound.

£1 is equivalent to two 50p coins.

£1 is equivalent to a 50p coin, two 20p coins plus a 10p coin.

£1 is equivalent to five 20p coins.

£1 is equivalent to ten 10p coins.

Any combination of coins that equals 100 pence is equivalent to one pound.

Any combination of coins that add up to 100 pence is worth £1.

Here is a downloadable summary sheet showing some of the different ways to make a pound.

Adding Pounds and Pence: Interactive Activity

Adding Pounds and Pence

We can count money more easily by separating it into pounds and pence.

We have three pounds made from the £2 plus the £1.

We have 90p made from the 50p plus the two twenty pence coins.

We can write the £3 and 90p as £3.90.

Supporting Lessons

How to Add British Money

Adding Pounds and Pence

Adding Pounds and Pence Interactive Activity

Adding Pounds and Pence with Carrying

Adding Pounds and Pence with Carrying: Interactive Activity

Counting Pounds and Pence Worksheets

counting pounds and pence worksheet answer pdf

Adding Pounds and Pence Harder Worksheets

Counting Money: Pounds and Pence

How to Add Pounds and Pence

To add pounds and pence coins use the following steps:

Separate the coins into pounds and pence.

Add the pound coins together to find the total number of pounds.

Gather the pence coins into groups worth 100 pence.

Each group of 100 pence is worth 1 pound, which can be added to the pounds total.

Count the remaining pence separately.

For example, here is a group of British coins, which we will add to find a total.

The first step is to separate the pound coins from the pence coins.

a collection of pound and pence coins

We have a two pound coin and a one pound coin.

2 + 1 = 3 and so £2 + £1 = £3. We have three pounds in pound coins.

We will now count the pence coins.

We have 50p + 20p + 20p.

50 + 20 + 20 = 90 and so, we have 90p.

3.90 shown by separating the pounds and pence before adding them up

In total we have £3 and 90p. We write this as £3.90.

To write pounds and pence, the pounds are written first, before the decimal point and the pence is written after the decimal point. £3 and 90 pence is written as £3.90.

counting pounds and pence example of 3 pounds 90 pence.

Here is another example of counting pounds and pence.

We first separate the pound and pence coins.

We have two one pound coins making a total of £2.

example of adding pound and pence coins with british money

Counting the pence coins, we have 50p + 20p + 10p, which equals a total of 80 pence.

In total we have £2 and 80 pence, which is written as £2.80. We separate the pounds and the pence with a decimal point.

How to Make a Pound with Coins

Here are some examples of how to make a pound using different pence coins:

100 × 1p

50 × 2p

20 × 5p

10 × 10p

5 × 20p

2 × 50p

Any combination of coins that add up to 100 pence are worth £1.

Here are some examples of how to make one pound.

how to make a pound using coins

We can add combinations of coins by grouping them into totals that equal 100 pence. Each group of 100 pence is worth a pound.

In this example we have a £1 coin along with two 50p coins and two 20p coins.

We have £1 in pounds and we will look for combinations of pence coins that add to 100 pence.

adding combinations of pounds and pence

We have two 50p coins which both add to make 100p. Two 50p coins are worth £1.

We have £2 in total and two remaining 20p coins. 20p + 20p = 40p.

In total we have 2 pounds and 40 pence. We write this as £2.40. The decimal point separates the pounds and the pence.

Here is another example of finding the total of a combination of coins.

3 pounds and 20 pence with ten 10p coins ready to be carried into the pounds

We have a £2 coin. We then look for combinations of coins that add together to make a pound.

We can see that we have ten 10p coins. 10 × 10p = 100p. Ten 10p coins are worth £1.

3 pounds 20 pence with one pound made up of ten 10p coins

adding pence coins to make pounds

In total we have £3 and 20 pence. We write this as £3.20.

Here is another example of adding penny coins.

We do not have any pound coins and so, we first look for groups of penny coins that add to make 100 pence.

adding penny coins to make a total

We have the combination of five 20p coins. Five times 20p equals 100p and so, five 20p coins are worth £1.

We have £1 and 19 pence, which is written as £1.19.

In this example, we have two pound coins and some pence coins.

counting coins example with pounds and pence

We look for a combination of pence coins that also add to make one pound.

It is easiest to start by adding the largest value coins. We start with 50p. We can add the two 20p coins to this 50p.

50p + 20p + 20p = 90p. We need 10p more to make 100 pence.

Therefore 50p + 20p + 20p + 10p equals £1.

We move these coins over to the pounds total. There is 10 pence remaining in the form of two 5p coins.

We have £3 and 10 pence, which is written as £3.10.

Sometimes we cannot make exactly one pound because we cannot make a group of exactly 100 pence.

Here is a collection of coins, with £2 in pound coins and some more pence coins.

adding combinations of coins

We cannot make 100 pence exactly so we look for a value that makes at least 100 pence.

We start with the 50p coin and add on the 20p coins.

50p + 20p = 70p.

50p + 20p + 20p = 90p.

50p + 20p + 20p + 20p = 110p.

We will move the 50p and the three 20p coins over to the pounds column. 110p is worth £1 and 10 pence.

adding pence coins to make a pound

In the pounds column, we have £3 and 10 pence. We have 24 pence in the pence column.

In total we have £3 and 34 pence, or £3.34.

the total of a collection of pence and pound coins

example of how to add coins

We can also add pounds and pence by writing the pounds in terms of pence.

Each pound coin can be written as 100 pence and then the totals can be added using column addition.

Here is an example of a collection of coins that will be added together to find a total.

The £1 coin will be written as 100 pence.

adding coins using column addition

The total can be found by adding the digits of each coin using column addition as shown below.

In the first column, we have 1 + 2 = 3.

In the next column, we have 2 + 5 = 7.

In the next column, we have 1.

In total, this is £1.73.

how to add money using column addition

Here is another example of adding money using column addition.

We have a £2 coin, two 10p coins and a 5p coin.

We write the £2 coin as being worth 200 pence.

We add 200p, 10p, 10p and 5p.

adding british money using column addition

In the first column, we have 5.

In the second column we have 1 + 1 = 2.

In the next column, we have 2.

In total we have £2.25.

If the coins can be easily counted into groups worth 100 pence, then it is easiest to group the coins into collections of pounds and add them.

For combinations of coins that cannot be made into pounds, then column addition can be an easier method for adding money.

Now try our lesson Reading Hours on a Clock where we learn how to tell the time to the hour.

Reading Hours on a Clock

Adding Pounds and Pence with Carrying: Question Generator

What is the total sum of the coins below? Enter your answer in pounds with a decimal point.

Click on each coin as you count it.

Adding Pounds and Pence: Question Generator

What is the total sum of the coins below? Enter your answer in pounds with a decimal point.

Click on each coin as you count it.

British Money: Learning Pound and Pence Coins

Counting British Penny Coins: Interactive Activity

List of all British Pence Coins

all british pence coins with pictures

Above are all of the coins used in the United Kingdom that have a value of less than one pound (100 pence).

List of the British Pound Coins

british pound coins with pictures

A one penny coin is the British coin of lowest value and is written as 1p for short.

A one pound coin is worth 100 pence and we write it with the symbol ‘£’.

ways to make 10p using penny coins

1 ten Pence is worth the same as ten 1p coins.

10p is also worth the same as 5p + 5p.

We could also make 10p from 5p + 2p + 2p + 1p.

Supporting Lessons

Learning the British Pence Coins Video Lesson

Learning the British Pound Coins Video Lesson

Interactive Money Activities

Adding Pounds and Pence: Interactive Activity

Counting Penny Coins Worksheet

counting uk pence coins worksheet answers pdf

Counting Pound Coins Worksheet

counting uk pound coins worksheet answers pdf

Counting British Coins: Adding Pounds and Pence

Learning the British Coins

Pictures of British Coins and their Values

In Britain, there are 6 different coins that are worth pennies and 2 different coins that are worth pounds.

Here is a list of all of the British Penny coins with their name and value shown below.

british penny coins and their value

In the UK, the coin with the lowest value is the 1 penny coin.

When we have more than 1 penny, we say that we have pence. So we have 2 pence, 5 pence, 10 pence, 20 pence and 50 pence coins.

The symbol for pence is ‘p’. This is because it is the first letter of the word pence.

We can write 1 penny as 1p, 2 pence as 2p, 5 pence as 5p, 10 pence as 10p, 20 pence as 20p and 50 pence as 50p.

In British money, the p is pronounced as ‘pee’ and is said after the number.

1 Penny Coin

The penny coin is the lowest value British coin. The penny coin is also known as 1 pence and is written as 1p for short. This is pronounced as ‘1 pee’.

british money one penny coin

2 Pence Coin

Here is a 2 pence coin. We say pence now, rather than penny because 2 is more than 1. We only say penny for the 1 penny coin. Whenever we have a coin that is worth more than 1 penny, the word penny changed to pence.

uk money two pence coin

We say that we have 2 pence, or 2p. This is pronounced as ‘2 pee’.

2p is worth the same as 2 1p coins

2p is worth the same as two 1p coins.

in british money two one penny coins are the same value as a 2 pence coin

1 + 1 = 2 and so, 1p + 1p = 2p.

5 Pence Coin

Here is a 5 pence coin.

a five pence british coin

5p is worth the same as five 1p coins.

5 pence is the same value as 5 one penny coins in the united kingdom monetary system

5 = 1 + 1 + 1 + 1 + 1 and so, 5p = 1p + 1p + 1p + 1p + 1p.

5p can be made from any combination of coins that add up to make 5p.

For example, 2 + 2 + 1 = 5 and so, 2p + 2p + 1p = 5p.

two two pence coins plus a one pence coin has the same value as a five pence coin

Here we can see that 5p = 1p + 1p + 1p + 1p + 1p and for every two pennies we have, they can be replaced with a 2 pence coin.

the value of a 2 pence coin

5p = 2p + 2p + 1p.

10 Pence Coin

Here is a 10 pence coin, or 10p.

10 pence british coin

10p is worth the same as 10 1p coins. It is much easier to carry 1 single 10p coin around instead of carrying ten pennies.

10 pence is worth the same as 10 one penny coins

the sum of ten one penny coins is worth ten pence

5 + 5 = 10 and so, 5p + 5p = 10p.

10 pence is worth the same as 5p + 5p

in UK money, two 5 pence coins are worth 10 pence

Any combination of coins that add to make ten pence can be replaced with a ten pence coin.

For example, 5 + 2 + 2 + 1 = 10 and so ten pence can be made from a 5p, 2p, 2p and a 1p coin.

the british coins of 5 pence, two two pence coins plus a one pence coin are equivalent to ten pence

combination of coins that add to 10 pence

20 Pence Coin

Here is the 20 pence coin.

a 20 pence coin in british money

20p is worth the same as 10p + 10p.

two 10 pence coins add to make 20 pence

20 pence is worth 10p + 10p

50 Pence Coin

Here is a 50 pence coin. The 50 pence coin is the largest coin in terms of size. The 50 pence coin is the pence coin with the largest value. There is no other coin that is worth more than a 50p apart from the pound coins.

united kingdom 50 pence coin

Any combination of coins that add to make 50 are worth the same as a 50 pence piece.

For example, 20 + 20 + 10 = 50 and so a 50 pence coin is worth the same as 20p + 20p + 10p.

50 pence is the sum of two 20 pence coins plus a 10 pence coin

50 pence is worth 20p + 20p + 10p

British Pound Coins

Here are the 2 different coins that are worth £1 and £2.

british £1 and £2 coins

1 pound is worth 100 pennies. Instead of 100 1p coins, a £1 coin can be used. Any combination of coins that add up to 100 pence can be replaced with a pound coin.

£1 = 100p

There are many different ways that we can make £1. We can make a pound by using any combination of coins that add up to 100p.

The £ symbol is the pound symbol. £1 is actually said with the number first and then the word pound. So we say £1 as ‘one pound’. We say £2 as ‘two pounds’.

For example, we can use two 50p coins to make a pound.

2 fifty pence coins are worth one pound

This is because 50p + 50p = 100p. 1 pound is worth the same as two 50 pence pieces

100p = £1

Another way to make £1 is to use a 50p coin, two 20p coins and a 10p coin.

making one pound with a fifty pence two twenty pence and a ten pence coin which add to make 100 pence

50p + 20p + 20p + 10p = 100p

100p = £1

a combination of coins that add to make 1 pound

Here we have a combination of coins that add to make £1. We can keep adding the total together until we have 100 pence.

Here is a £2 coin.

a two pound coin

The 2 pound coin is worth the same as 2 pound coins combined. A 2 pound coin is worth 200 pence.

2 pound coin is worth the same as two pound coins

Each pound is worth 100p and so 100p + 100p = 200p.

a 2 pound coin is worth the same as two 1 pound coins combined

£2 = 200p and so any combination of coins that adds to 200 pence can be replaced with a £2 coin.

For example we have £1 + 50p + 50p.

a combination of coins that add to make 2 pounds

The £1 is worth 100p. 100p + 50p + 50p = 200p, which is the same value as £2.

a sum of coins that add to make 2 pounds

It is helpful to group combinations of coins that make £1. Counting pounds can be easier than counting pennies with larger amounts of money.

In this example, the two 50p coins can be combined to make £1.

£1 + £2 + £1 = £4.

counting pound coins

Now try our lesson Counting British Coins: Adding Pounds and Pence where we learn how to add different groups of British coins.

example of some british coins

Understanding Ratios with Examples and Pictures

visual explanation of a ratio of dogs to cats

A ratio tells us how many of one object there are compared to another.

There are 3 cats and 5 dogs, which makes 8 animals in total.

We say there are 3 cats to every 5 dogs in this picture.

We write the numbers of each object as a ratio, separated by a colon ‘:’.

The ratio of cats to dogs is 3:5.

We read this as ‘3 to 5’

It is important to write the numbers in the same order in which they are mentioned.

Writing the ratio the other way around, the ratio of dogs to cats is 5:3.

We write the number of each object separated by a colon sign ‘:’. .

introduction to ratios

We count the number of each coloured counter.

We have 3 blue counters.

We have 2 purple counters.

We say that we have 3 blue to 2 purple.

We write the ratio of blue to purple as 3:2.

Supporting Lessons

Understanding Ratios Worksheets and Answers

$converting ratios to fractions worksheet and answers$