In this lesson we are comparing numbers and writing comparison symbols in between the numbers to show which is the larger number.

The symbol for ‘greater than’ is ‘>’.

The symbol for ‘less than’ is ‘<'.

The way to remember which sign to use is that the symbol will point at the smaller number like an arrow.

Another way to remember greater than or less than signs is that the open end of the symbol will be facing the larger number. We can imagine the symbol like a crocodile’s open mouth and then remember that the crocodile will want to eat the largest number to have a larger meal.

In this lesson we will write the comparison symbols of ‘greater than’ and ‘less than’ to compare two numbers.

We will begin with our first comparison symbol, the equals sign.

• Equals Sign (=):

The equals sign means ‘the same value as’.

For example:

3 + 1 = 4

4 = 4

This is telling us that 3 + 1 has the same value as four.

• Greater Than Sign (>):

The greater than sign means ‘bigger than’ or ‘larger than’.

For example:

5 > 4

We read this as ‘five is greater than four’.

• Less Than Sign (<):

The less than sign means ‘smaller than’.

For example:

4 < 5

This is read as ‘four is less than five’.

We will use some examples of greater than or less than signs to look at ways to remember the direction in which the greater and less than signs are drawn when comparing two numbers.

To determine if a number is greater than or less than another number we can look at a number line.

The further we go to the right on our number line, the larger our number.

A number is greater than another number if it is further to the right of it on the number line.

Greater Than Example:

In the example below, we can see that 3 is a larger number than 1. So, we say that three is greater than one.

One way that we can remember which sign to put in between the numbers is to think of the comparison sign as an arrowhead. This arrowhead points to the smaller number.

So, it points to 1.

Another way to remember which symbol is the greater than sign, is to think of the symbol as a crocodile.

The crocodile is hungry and wants to eat the larger number. So, its mouth opens towards 3.

Less Than Example:

In the example below, we can see that 6 is a smaller number than 8.

We know this because 6 is on the left of 8 on the number line.

So, we say that six is less than eight.

We can use the same two methods that we used previously to remember which comparison sign represents ‘less than’.

Think of the symbol as an arrowhead which always points towards the smaller number. So, it points towards 6 rather than 8.

We could also think of the less than sign as a crocodile that wants to eat the larger number. So, its mouth opens towards 8.

When teaching greater than and less than signs, the biggest mistake is writing the symbols the wrong way around.

Fortunately, the signs are the same shape, just in reverse directions.

The best way to remember the direction is that the sign will point at the smallest number like an arrow.

Rules for Adding and Subtracting Negative Numbers

The rule for adding and subtracting negative numbers is to add the numbers if the signs are the same and to subtract the numbers if the signs are different.

If there are two negative signs or two postive signs, then perform an addition. If there is a positive and negative sign in any order, then perform a subtraction.

Here is a guide to the rules for adding and subtracting directed numbers.

We can think of the negative sign as having an opposite effect. A negative sign will change the sign next to it to have the opposite effect.

In the case of ‘- -‘, the first negative sign changes the negative sign it is next to into a ‘+’. There are four rules for adding and subtracting negative numbers, which are:

	Signs	Rule
Same signs	+ and +	Add the numbers
	– and –
Different signs	+ and –	Subtract the numbers
	– and +

These rules are used when there are two signs next to each other in an equation.

For example, 10 + – 4 can be written as 10 – 4, which equals 6.

17 – + 6 can be written as 17 – 6, which equals 11.

In these examples, the combination of ‘+ -‘ or ‘- +’ were replaced with a single subtraction.

Here is an example of subtracting a negative number. We have 2 – – 5. The two signs ‘- -‘ are the same, so we will be performing an addition.

Two negative signs are replaced with a single addition.

2 – – 5 is the same as 2 + 5, which equals 7.

The final case shows two positive signs being replaced with one.

For example, 6 + + 3 is the same as 6 + 3, which equals 9.

There is no need to write two plus signs in this sum.

Adding a Negative Number

To add a negative number, simply ignore the negative sign and subtract it from the other number instead of adding it.

For example, here is 15 + – 7. We have a positive number add a negative number. We are adding negative 7 to positive 15.

Replace the ‘+ -‘ in a sum with a single ‘-‘ sign.

15 + – 7 is the same as 15 – 7.

15 – 7 = 8 and so, 15 + – 7 = 8.

To understand why adding a negative number is the same as a subtraction, we can consider negative numbers as ice cubes. By adding an ice cube, the temperature drops. By adding a negative, the value of the number drops.

Here is a drink that measures 7 degrees.

We will think of our negative number (-1) as an ice cube.

Adding an ice cube makes the drink colder and so, the temperature goes down.

7 – 1 = 6 and so, adding the ice cube resulted in a subtraction.

We can write 7 + – 1 = 6 or we can write the negative number in brackets as 7 + (-1) = 6.

It does not matter if a negative number is written in brackets or not. Writing the bracket can make it easier for some people to visualise the negative number in this ice cube analogy and also to show that the negative sign belongs to the 1. However, not writing the bracket can make it easier to see the ‘+ -‘ combination and more easily replace it with a ‘-‘.

If instead of adding 1 ice cube, we add 3, then the temperature will drop by 3 instead of 1.

Each ice cube lowers the temperature by 1. Each ice cube is worth (-1).

The drink was 7 degrees to begin with. Adding three ice cubes can be shown with the sum 7 + – 3.

The temperature goes down by 3 to get to 4.

7 + – 3 = 4 because 7 – 3 = 4.

It does not matter which order the positive and negative signs are written. Both + – and – + are replaced with a -. If there is a positive and negative sign together, the result is a subtraction.

Here is an example of 8 – 5. The 5 can be written as positive 5 or + 5.

We can write 8 – 5 as 8 – + 5 or even as 8 – (+ 5). We don’t normally write the plus sign in front of the 5 because we assume a number is positive unless told otherwise.

8 – 5 = 3 and so 8 – + 5 is also equal to 3.

The ‘- +’ is the same as a ‘-‘ sign. The ‘- +’ is replaced with a subtraction.

Subtracting a Negative Number

To subtract a negative number from another number, ignore any negative signs and add the numbers together.

For example, here is 10 – – 4. Ignoring the negative signs, we have 10 and 4. We add 10 and 4 to get 14. Therefore, 10 – – 4 = 14.

If two negative signs are next to each other, we can replace them with a positive sign. ‘- -‘ can be replaced with a ‘+’.

Here is another example of subtracting a negative number. We have 8 – – 3.

It can be helpful to circle any double negatives and write an addition sign above.

8 – – 3 can be written as 8 + 3, which equals 11. 8 – – 3 = 11.

To understand why subtracting a negative number results in an addition, we can consider the negative number as an ice cube. Removing an ice cube can make the temperature go up. Removing a negative number can make the value of the number go up.

Here is a drink which contains an ice cube. Its temperature is 5 degrees.

If the ice cube is removed, the temperature will increase. If the ice cube is cooling the drink by 1 degree, then removing it will warm up the drink by 1 degree.

The drink was 5 degrees and is now 6 degrees. 5 + 1 = 6 and so 5 – – 1 = 6.

We can see that the ‘- -‘ in 5 – – 1 = 6 can be replaced with a ‘+’ to make 5 + 1 = 6.

Here is a different drink which contains 3 ice cubes. It is currently 5 degrees.

We will remove all three ice cubes to make the temperature go up by three.

5 + 3 = 8 and so, 5 – – 3 = 8.

Two negative signs make a positive because one negative sign creates the opposite effect in the other negative sign. The effects in each of the two negative signs cancel out to produce a positive effect.

Teaching Adding and Subtracting Directed Numbers

To teach directed numbers, it is important to begin with real life analogies. Some examples include:

• Removing an ice cube causing the temperature of a drink to increase.
• Removing a weight can cause something to go upwards
• Removing a bill or debt means that you have more money to spend.

When teaching adding and subtracting negative numbers in general, it is useful to encourage the circling of the combinations of positive and negative signs before replacing them with a + or – sign. This can build up a longer term strategy which is not so easily forgotten.

With several different negative number rules to remember, it is important to get lots of practice with each method and having written strategies can help with this.

Children can sometimes forget to use this procedure and could believe the sum to be more complicated than it is. By getting them in the habit of circling the two signs and replacing them with a single operation, there is more structure for tackling the question.

Odd numbers cannot be halved to give a whole number. We will look at methods we can use for teaching halving odd numbers.

In our first example of halving odd numbers, we are asked to halve the number five. We’ll start by looking at the method of division by sharing. We can represent the number five with five counters. We want to halve it, which means that we want to share it equally across two groups.

We can easily halve four of the counters by placing two in each group, since 4 is even. However, there is one counter remaining in the middle. If we put this whole counter in either of the groups, we would not have shared five equally.

The only way that we can share this last counter equally is to split it in half.

Each half can then be placed in each group. Each group contains 2    ¹ / ₂   counters.

Therefore, half of 5 is 2  ¹ / ₂  .

When first introducing halving odd numbers and teaching halving to your child, you could show this easily with plasticine or food, tearing the last item in half.

Starting again with our five counters, we can develop a method to work out halving an odd number mentally.

We found that it was easy to halve the counters when the number was even.

We were able to halve four of the counters easily. So, we can begin by subtracting 1 from our odd number.

Subtracting one from every odd number will always give us an even number.

• Step 1: Subtract 1

5 – 1 = 4

Now that we have an even number, we can easily halve it.

• Step 2: Halve it

4 ÷ 2 = 2

We have easily divided the four counters into two groups.

Now, we must remember that one counter that we previously subtracted.

• Step 3: Add  ¹ / ₂

The ‘1’ that we originally subtracted must also be halved. Half of 1 is    ¹ / ₂.

So, we must add this on to the 2.

2 +  ¹ / ₂ = 2  ¹ / ₂

Half of 5 is 2  ¹ / ₂.

Another way of thinking of this is that we were able to partition the 5 into 4 + 1.

Half of 4 is 2

Half of 1 is    ¹ / ₂

2 +  ¹ / ₂ = 2 ¹ / ₂

Now we’ll look at another example of halving odd numbers where we will use our three steps.

We are asked to find half of 7.

We can work out this example of halving an odd number by partitioning 7 into 6 + 1.

We do this in the following three steps.

• Step 1: Subtract 1

7 – 1 = 6

We subtracted 1 to give us an even number to halve.

• Step 2: Halve it

6 ÷ 2 = 3

• Step 3: Add    ¹ / ₂

3 +    ¹ / ₂ = 3   ¹ / ₂

We add  ¹ / ₂   because this is half of the ‘1’ that we originally subtracted.

We worked this out by partitioning the 7 into 6 + 1. This partitioning method is the easiest to do mentally when teaching your child to halve odd numbers.

First, we halved the 6.

Half of 6 is 3

Next, we halved the 1.

Half of 1 is    ¹ / ₂

Finally, we added these together.

3 +  ¹ / ₂ =  ¹ / ₂

Even numbers are in the two times table.

Even numbers can be arranged in pairs. This means that they can be divided into two equal parts, or halved exactly.

The whole numbers are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 … onwards.

We will look at these numbers in this lesson and we will start by looking at zero.

The definition of an even number is a whole number that can be halved exactly to leave another whole number.

Half of zero is zero.

And zero is a whole number.

Therefore zero is an even number.

When teaching odd and even numbers, it can be common for a child to be unsure as to whether zero is odd or even so it is important to tell them specifically that zero is actually even.

We will now look at our next example of an even number:

Two is an even number. It can be halved exactly to equal one.

2 x 1 = 2

Two is in the two times table and so it is even.

Four is an even number. It can be arranged a pair. When divided into two equal parts, each part is worth 2 because 4 ÷ 2 = 2.

2 x 2 = 4

Four is in the two times table and so it is even.

Six is an even number. It is in the two times table. It can be divided by two to equal three.

Eight is an even number. It is in the two times table and we can see that it can be arranged in pairs.

Eight is two pairs of 4.

Ten is an even number. It can be halved to form two groups of five.

We can see from our list of even numbers so far that they start at zero and there is a difference of two between each even number.

If we have an even number and we add two, we will be at another even number.

Odd numbers are not in the two times table.

Odd numbers cannot be arranged in pairs. This means that they can’t be divided into two equal parts, or halved to give a whole number.

One is an example of an odd number:

One is the first odd number. It can’t be arranged in pairs.

Three is an odd number. It can’t be divided into two equal parts (where each part contains a whole number).

Three is not in the two times table.

Five is an odd number. It is not in the two times table.

Seven is an odd number. It can’t be halved (to give a whole number).

Nine is an odd number. It is not in the two times table and therefore can’t be divided into two equal parts (where each part is a whole number).

Below is a summary of the even and odd numbers from one to ten. You will notice that the numbers alternate between being even and odd.

Every time we add one we change from being odd to even or even to odd.

We can think of the even numbers as being the numbers in the two times table and then the odd numbers are the numbers that are in between the even numbers.

We are going to count the number of dogs.

To do this we start at zero on the number line and move along one place for every dog that we count.

We can point at each dog and say the number as we count it.

We will then cross off each dog after we say the corresponding number so that we don’t count it twice. This can be more important with larger numbers and in our image below, the dogs are spaced out in no particular order.

We count ‘1’ and cross out a dog.

We count ‘2’ and cross out another dog.

We count ‘3’.

We count ‘4’.

We count ‘5’.

We continue to move along the number line.

…6, 7, 8…

We continue to cross of each dog as we count it.

…9, 10, 11…

…12, 13, 14…

…15, 16, 17…

…18, 19, 20.

We have now counted all of the dogs.

The last number that we say as we cross off our last dog is 20.

There are twenty dogs altogether.

In the next example, we will count the number of snakes.

We will count the following snakes by counting up on ones and crossing off each snake as we count it.

There are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.

There are ten snakes altogether.

Some more snakes appear. So, we start at 10 and count up in ones as we move along the number line. We will continue to cross off each snake as we count it.

We count ‘11’ and cross out a snake.

We count ‘12’ and cross out a snake.

We count ‘13’ and cross out another snake.

We continue to count up in ones, crossing off each snake as we count it.

…14, 15, 16…

…17, 18, 19…

We have crossed off all of the snakes. This means that we have counted all of them. There are nineteen snakes altogether.

In this lesson we are going to learn how to count to ten. We will be looking at some examples that will help you teach your child to count.

We will be counting the numbers of animals that we have in these examples. We will look at numbers ranging from zero to ten, using a number line to help us.

We are going to count the number of birds in the following example:

Before we even start counting any of the birds, we first start at zero on our number line.

When teaching your child to count, it is helpful to tell them that we first start at zero. You could ask them to put their finger on the zero place on the number line.

As we count the birds, we will move along the number line, one number at a time.

We would certainly recommend your child knowing how to say the numbers one to ten in order by memory before actually counting anything.

If your child is familiar (preferably fluent) with saying the sequence:

1, 2, 3, 4, 5, 6, 7, 8 , 9, 10

verbally, then the actual process of counting will be much easier.

If we were counting physical items, we could always move each item to one side as we count it, however we will not always be able to do this.

When teaching your child to count, we can consider some important strategies to help them.

Only say one number for each object that we count (it can be helpful for your child to physically point at each bird as they say each number).

If they say more than one number as they count one bird, start again.

We will cross out each bird after we count it and say the number, so that we don’t count the same bird more than once. We say ‘one’ as we point at the bird and cross it off afterwards.

We count the next bird by moving along the number line. We count two.

Next, we count the final bird by moving along the number line to three.

We cross off this bird after we say the number ‘three’.

Since we have crossed off all of the birds, we stop. ‘Three’ was the last number that we said, therefore there are three birds altogether.

It would be worth showing your child the same process as we move along the number line at the top.

We counted the birds by starting at zero and moving one place along the number line for every bird. We counted one, two, three.

In the next example, we will count the number of dogs.

Remember that we start at zero and it is worth saying zero with your child before you start counting.

We count the first dog as ‘1’ and cross it out after we say the number.

We count the next dog as ‘2’ and cross it out after we say the number.

We count ‘3’ and cross out the next dog after we say the number.

We count ‘4’ and cross out another dog.

We count ‘5’ and cross out the final dog.

There are five dogs altogether. Remember once we have crossed out all of the animals, we can stop counting.

When teaching your child to count drawn objects, you could cross out drawings on paper. If you are teaching your child to count physical counters, you could move the counters as you count them.

As your child practises counting, we slowly move on to counting without crossing out and saying the number out loud as their eyes track to the next object, rather than pointing.

In the final counting example, we will count the number of snakes.

Again, we will start at zero and move one place along the number line for each snake that we count.

We count ‘1’ and cross out a snake.

We count ‘2’ and cross out another snake.

We count ‘3’ and cross out a snake.

We count ‘4’.

We count ‘5’.

We count ‘6’.

We count ‘7’.

Finally, we count ‘8’.

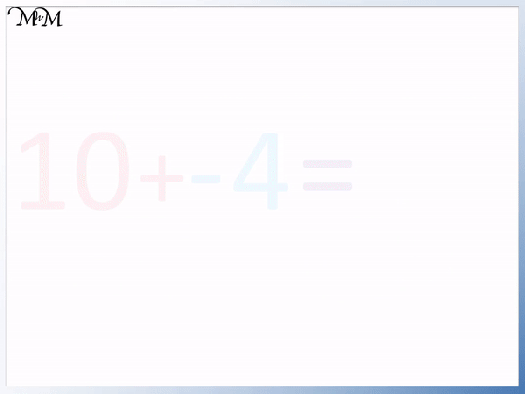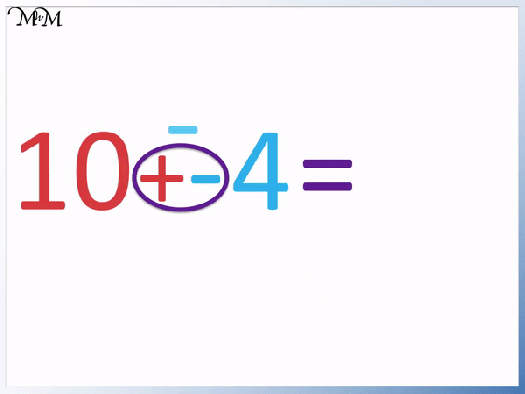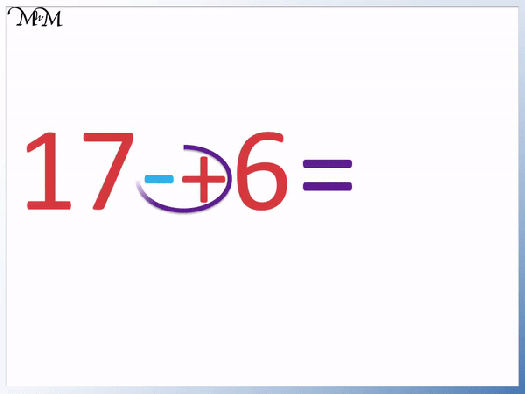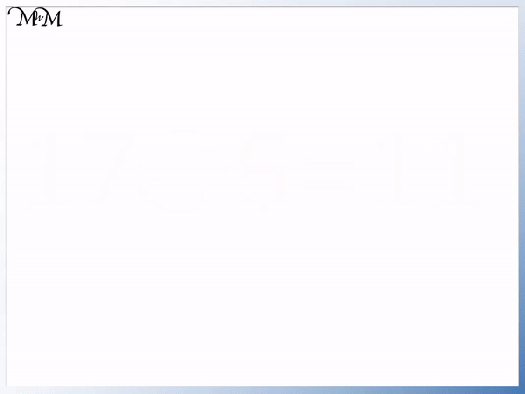
We have now counted all of the snakes. Therefore, there are eight snakes altogether.

How to Find the Volume of a Cuboid

To find the volume of a cuboid, multiply its length, width and height together in any order. The units of the length, width and height need to be the same and this unit is cubed in the final volume answer.

For example, a cuboid with a length of 5 cm, a width of 2 cm and a height of 3 cm has a volume of 5 x 2 x 3 = 30 cm³.

It does not matter in which order the numbers are multiplied together. 5 x 2 x 3 and 2 x 3 x 5 both equal 30.

The length, width and height of a cuboid must be right angles to each other. When finding the volume of a cuboid, it is important to make sure that the 3 dimensions of length, width and height are all at right angles to each other when measuring them. It is possible to make the mistake of reading the wrong dimension and read one of the dimensions twice.

The height of a cuboid is always measured as the vertical distance from the bottom to the top. In this example, the height is 3.

Aside from the height, there are two remaining sides. The length is the longest side and the width is the shortest side.

The length of this cuboid is 5 and the width is 2.

The Formula for the Volume of a Cuboid

The formula for the volume of a cuboid is V = l x w x h, where l is the length, w is the width and h is the height. This formula can be written more concisely as V = lwh. The volume is in cubic units.

The volume of a cuboid is length x width x height. This equation can be simplified into a formula by replacing length with the letter l, width with w and height with h.

V = l x w x h

We don’t tend to write multiplication signs when using algebra. Writing the formula V = l x w x h without multiplication signs allows us to write the formula for a volume of a cuboid in its simplest form as V = lwh.

A cuboid is also known as a rectangular prism. Therefore finding the volume of a rectangular prism is the exact same method used for finding the volume of a cuboid.

To find the volume of a rectangular prism, multiply the length, width and height together in any order. For example, a rectangular prism with a length of 4 cm, a width of 3 cm and a height of 2 cm has a volume of 4 x 3 x 2 = 24 cm³.

The formula for the volume of a rectangular prism is V = l x w x h.

Volume of a Cuboid by Counting Cubes

The volume of a cuboid can be found by counting how many centimetre cubes its contains. It is easiest to count the cubes in one layer and then to multiply this by the number of layers in the cuboid.

A cuboid has three dimensions. The dimensions are the height, length and width.

Here is a cuboid with only one layer.

There are twelve cubes in total. We know this because the length is 4 and the width is 3. To find the number of cubes in each layer of a cuboid, multiply the length by the width. 4 x 3 = 12 and so, there are 12 cubes in this layer.

The volume of this cuboid is 12 cubic centimetres, 12 cm³.

When teaching volume by counting cubes, it is useful to have some physical cubes on hand to make the shapes with. The number of cubes can easily be counted as they are added.

Here is another cuboid, which is the same as before but has an extra layer.

The number of cubes in each layer has not changed. The length is still 4, the width is still 3 and so, the number of cubes in each layer is 4 x 3 = 12.

However we now have two layers of 12. 2 lots of 12 is found by multiplying 2 and 12. 2 x 12 = 24.

The volume of this cuboid is 24 cm³, 24 cubic centimetres.

Here is a cuboid with 3 layers. There are still 12 cubes in each layer.

We have 3 layers of 12 cubes. 3 x 12 = 36 and so the volume of this cuboid is 36 cm³, 36 centimetres cubed.

The number of cubes in each layer can be seen by looking at the cuboid directly from the top.

The volume of a cuboid is given by length x width x height. The length x width tells us the number of cubes in each layer of the cuboid and the heigth tells us how many layers there are. Multiplying the three dimensions together tells us the total number of centimetre cubes and hence, the volume in cubic centimetres.

Units of Volume for a Cuboid

The length of each side of a cuboid can be measured in centimetres, metres or any other unit of length. The units of measurement for volume must be this unit of length cubed.

For example, if the side of a cuboid is measured in centimetres, then the volume is measured in centimetres cubed (cm³).

If the side of a cuboid is measured in metres, then the volume is measured in metres cubed, (m³).

The small three in the unit of measurement is pronounced as ‘cubed’. This number tells us how many dimensions (directions) have been multiplied together.

For example, here is a rectangle with a length of 4 cm and a width of 3 cm. Its area is found by multiplying the length and width. 4 cm x 3 cm = 12 cm².

In the calculation of 4 cm x 3 cm = 12cm², we multiply a centimetre by a centimetre. To show that two centimetres lengths are multiplied together, we write 12 cm². The 2 shows us that 2 lengths were multiplied to get this result.

If we have one row of twelve 3D cubes, then we have a volume of 12 cm³.

This shape is now 3D. A 3 dimensional shape can be physically held as it has length, width and height. There is only one layer of cubes, so this shape has a height of 1.

The volume is found by 4 cm x 3 cm x 1 cm = 12 cm³.

When finding the volume, three sides measured in centimetres are multiplied together and so, the units of volume are cm³.

Here is a cuboid with three layers of 12.

The volume is 4 cm x 3 cm x 3 cm = 36 cm³.

Again, we multiplied the length, width and height together. Multiplying in 3 directions means that a three is needed as the power of our units.

cm x cm x cm = cm³.

cm³ is pronounced as centimetres cubed or cubic centimetres.