Short division is also sometimes instead referred to as the bus stop method.

The short division method is the most common written method introduced in primary school for dividing larger numbers.

To do the short division method, use the following steps:

1. Write the number being divided and consider each of its digit from left to right.
2. Divide each digit in the number separately by the number being divided by.
3. Write the answer to each of these divisions above each digit.
4. If the division is not exact, write the greatest number of times that the dividing number divides into this digit.
5. Write the remainder as a ten for the next digit along.
6. Continue to divide each digit until you reach the final digit.

We will start by looking at a simple short division example.

Here we have 482 ÷ 2.

We start the method by writing 482 and 2, separated by a line.

The next step in the short division method is to divide each digit by 2.

4 ÷ 2 = 2 and so, we write this ‘2’ above.

The next digit is an 8.

8 ÷ 2 = 4 and so, we write ‘4’ above.

Our final digit is 2.

2 ÷ 2 = 1 and so, we write a ‘1’ above.

482 ÷ 2 = 241.

Here is the full short division process.

Since the answer is a whole number and the division was exact, we say this short division has no remainders.

Here is another example of short division.

We have 585 divided by 5.

The first step is to divide the first digit in 585 by 5.

5 ÷ 5 = 1.

We next divide the second digit in 585 by 5.

This time 5 does not divide exactly into 8. We write down the greatest number of times that 5 goes into 8.

5 goes into 8 once.

8 ÷ 5 = 1 remainder 3.

We have a remainder of 3 because we need 3 more to get from 5 to 8.

We write the ‘1’ above and write the remainder of ‘3’ next to the following digit.

We now treat the ‘3’ and the ‘5’ as a ’35’.

We now have 35 ÷ 5.

35 ÷ 5 = 7.

Here is the full short division method.

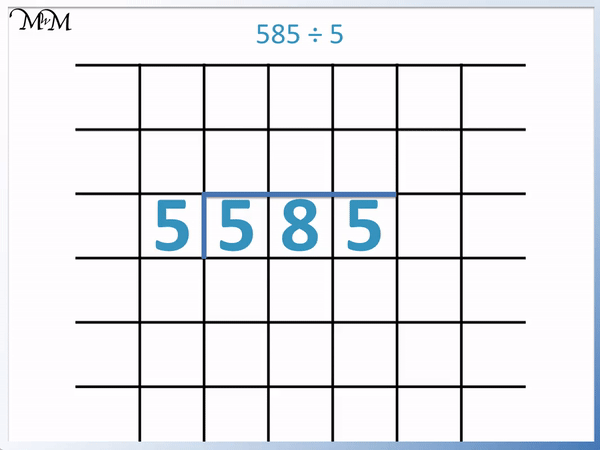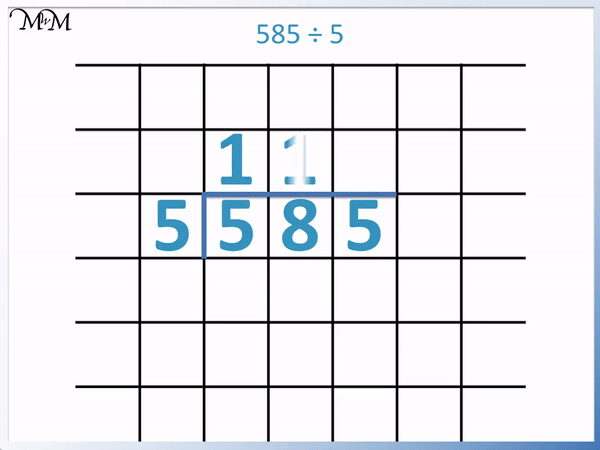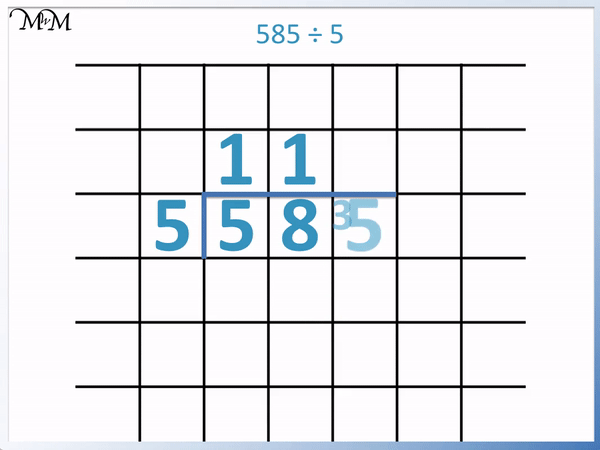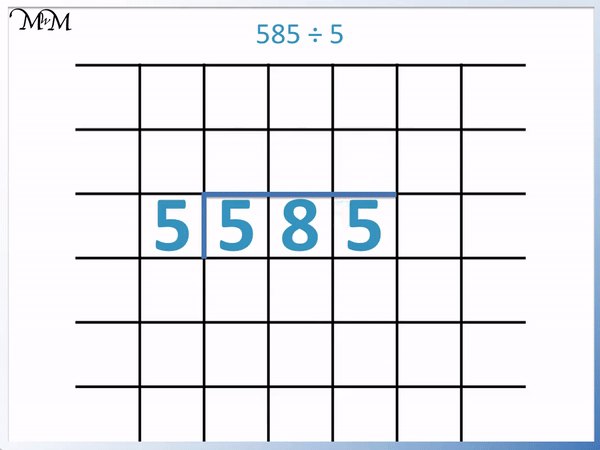
Since 5 divides exactly into 585, we say that this is an example of short division without remainders.

In this next example we have 148 ÷ 2.

Our first step is to divide ‘1’ by 2.

2 is larger than 1 and so it does not divide into ‘1’ even once.

We write a ‘0’ to show this and carry the ‘1’ over as a remainder.

The ‘1’ and the ‘4’ can be read as ’14’.

The final digit is ‘8’.

148 ÷ 2 = 74.

Since 2 goes exactly into 148 seventy-four times, we say that this short division has no remainders.

In this next example we have 432 ÷ 4.

4 ÷ 4 = 1 and so we write a ‘1’ above.

4 does not divide into 3 because 4 is larger than 3.

We write a ‘0’ to show that 4 divides into 3 zero times.

We carry the ‘3’ over to meet the ‘2’ in the next column. This is read as ’32’.

32 ÷ 4 = 8 and so, we write an ‘8’ above.

432 ÷ 4 = 108.