What is a Composite Shape?
A composite shape, or compound shape, is a more complex shape made from two or more basic shapes.
Composite shape questions seen in school are most often formed from a combination of rectangles, triangles and sometimes semi-circles.
In this lesson, we are looking specifically at compound shapes made entirely from rectangles.
This is an example of compound shape made only from rectangles.

We can see in the image below that the composite shape can be made from 2 rectangles.
The shape could also be described as an L-shape. It looks like a backwards capital L.
Sometimes these shapes may be informally described as an L-shape and whilst it is not their proper name, it allows us to easily recognise this style of composite shape.
L-shaped composite shapes are made from two rectangles.

A rectilinear shape is a shape in which all sides meet at right angles.
More simply, a rectilinear shape must be made only from rectangles.
Since this lesson is looking at compound shapes made from rectangles, all shapes that we are looking at will be examples of rectilinear shapes.
Finding the Area of Rectilinear Shapes
To find the area of a rectilinear shape:
- Split the shape into separate, non-overlapping rectangles.
- Find the area of each rectangle by multiplying its base by its height.
- Add the areas of each rectangle together to find the total area.
An L-shape is a common rectilinear shape that we see.
Below is an example of an ‘L-shaped’ compound shape.

To find the area of the L-shape, split it into two rectangles.
The L-shapes can always be split into two rectangles where one rectangle makes the vertical line of the ‘L’ and the other rectangle makes the horizontal line of the ‘L’.

The next step is to work out the area of each rectangle by multiplying their base by their height.
The left rectangle base is 5 cm and its height is 3 cm.
We multiply 3 cm by 5 cm.
3 × 5 = 15 and cm × cm = cm2. The units for area are cm 2.
Its area is 15 cm 2.
We now find the area of the right rectangle.

The base is 2 cm and the height is 6 cm.
2 × 6 = 12 and so, the area of this rectangle is 12 cm2.
We finally add the two areas together to find the total area of the composite shape.
15 + 12 = 27 and so, the area of the compound shape is 27 cm2.

Here is another compound L-shape example.
Before dividing the compound shape into two rectangles, we choose the rectangles so that we have the height and base of both.
We divide the rectangle as shown.
The base of the bottom rectangle is 10 cm and the height is 6 cm.
Its area is 6 × 10 = 60 cm2.
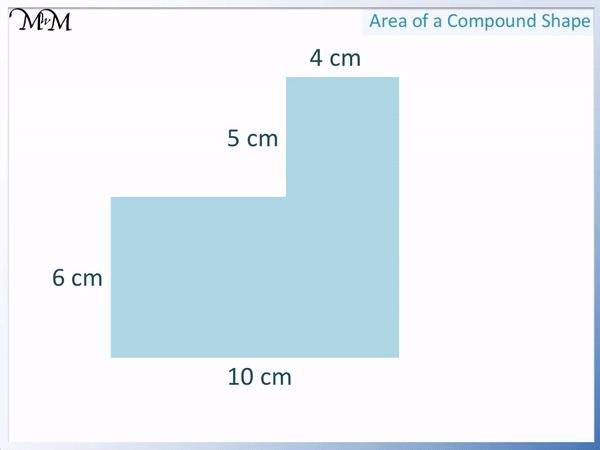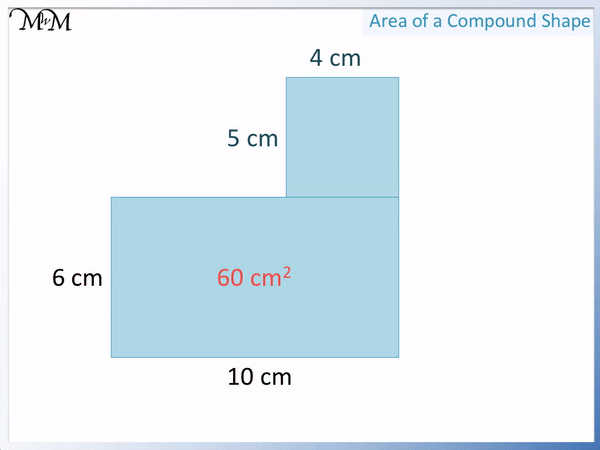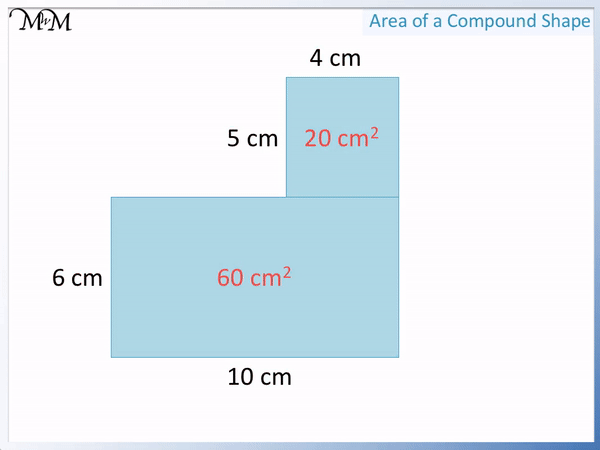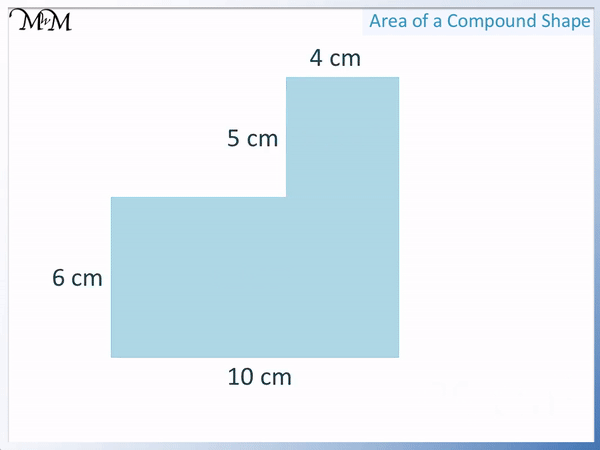
The base of the top rectangle is 4 cm and its height is 5 cm.
Its area is 4 × 5 = 20 cm2.
We add the two areas together to find the area of the composite shape.
60 + 20 = 80 cm2.
Notice that we split the L-shape in this way so that the base and height of each rectangle were already labelled for us.
How to Find the Area of Compound Shapes with Missing Sides
We can find the area of compound shapes by finding the area of each of the basic shapes that make it and then adding them up.
Sometimes we need to work out the lengths of sides that have not been given to us. If a compound shape has missing sides, then the first thing to do is to work them out by comparing them to other sides of the shape.
Here is an example of a composite shape with missing side lengths.
We can see that we have sides of 6 cm, 12 cm, 14 cm and 8 cm but we do not have the two sides shown in the bottom right of the shape.

We can split the shape into 2 rectangles.
The leftmost rectangle area is 6 × 12 = 72 cm2.

However we can see that in the next rectangle, we do not have the length of the base side shown.
The height is 8 cm but we must work out the base.

To find the missing side of a shape, compare its length to the length of a parallel side.
We can see in the image below that the red arrow and blue arrow shown must be as long as the top side.
The top side is 14 cm and the blue arrow is 6 cm.

14 – 6 = 8 and so, the red arrow side must be 8 cm.
We can now work out the area of this rightmost rectangle by multiplying the base and the height.
8 × 8 = 64 and so the area of the rightmost rectangle is 64 cm2.

We finally add the areas of the two rectangles together.
We have 72 + 64.
70 + 60 = 130 and 2 + 4 = 6.

72 + 64 = 136 and so the total area of this compound shape is 136 cm2



















